Page 111 - 2023年第54卷第3期

２
平均水力半径，ｍ、平均过水断面面积，ｍ ；Ｌ为管道或明渠长度，ｍ。
根据式（ １０）和（１１），可依次求解时段 Δ ｔ内每段管道或明渠的流量和每个节点的水头。
（ ３）雨水泵站调蓄池水量与污染物质量守恒约束：雨水泵站调控应满足蓄水池的水量平衡和污染
物质量平衡，其中，污染物质量平衡采用完全混合一阶衰减模型。同时，蓄水池水深变化应满足调蓄
池的调蓄容量，计算公式如式（ １２）—（１４）所示：
Ｉ ＋ Ｉ Ｏ ＋ Ｏ ２
１
２
１
Ｖ－ Ｖ ＝ Δ ｔ － Δ ｔ （１２）
２
１
２ ２
Ｉ
Ｉ
ＣＩ ＋ ＣＩ ＣＯ ＋ ＣＯ ２ ＣＶ＋ ＣＶ
１ １
２ ２
１ １
２ ２
１
１
２
－ ３
－ ３
－ ３
－ ３
１０ ·（ＣＶ－ ＣＶ） ＝１０ · Δ ｔ － １０ · Δ ｔ － １０ ·ｋ Δ ｔ ＋ Ｐ （１３）
１ １
２ ２
２ ２ ２
Ｄ ＜Ｄ＜Ｄ ｍａｘ （１４）
ｔ
ｍｉｎ
式中：脚标 １、２分别表示一个时段（ Δ ｔ）调蓄池对象特征值的初始值和终值；Ｖ、Ｖ为调蓄池容积的
１ ２
３
３
３
前后变化，ｍ ；Ｉ、Ｉ为调蓄池入流的前后变化，ｍ ?ｓ；Ｏ、Ｏ 为调蓄池出流的前后变化，ｍ ?ｓ；Ｃ、
１ ２ １ ２ １
Ｉ
Ｉ
Ｃ为调蓄池出流污染物浓度的前后变化，ｍｇ?Ｌ；Ｃ、Ｃ为调蓄池入流污染物浓度的前后变化，ｍｇ?Ｌ；ｋ
２
１
２
为 Δ ｔ时刻的污染物降解系数；Ｐ为 Δ ｔ时刻的污染负荷源汇项，ｋｇ；Ｄ为 Δ ｔ时刻的调蓄池水深，ｍ；
ｔ
Ｄ 和 Ｄ 分别为调蓄池的允许最低水深和最高水深，ｍ。
ｍｉｎ ｍａｘ
２．２ 决策变量 对于已建成的城区雨水泵站而言，排水泵的运行方式是最有效的人工调控手段，也是
在优化过程中寻找满足内涝防控、污染削减且经济可行方案的重要决策变量。排水泵的运行方式不仅
通过控制排水量直接影响雨水泵站蓄水池内的水量变化和排污量，而且还通过蓄水池容积变化间接影
响节点积水累计时间。因此，本研究选取每个水泵的启闭水深作为决策变量。
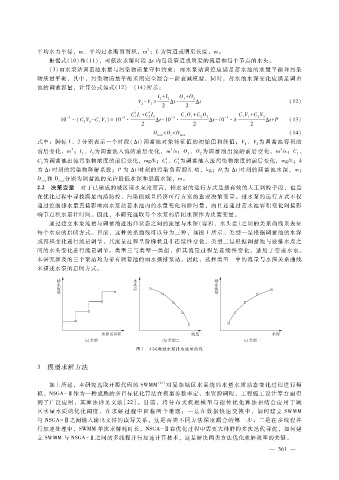
通过建立水泵流量与调蓄池进出口状态之间的流量与水深（容积、水头差）之间的关系曲线来表征
每个水泵的启闭方式。目前，这种关系曲线可以分为三种，如图 １所示。类型一是根据调蓄池的水深
或容积变化进行流量调节，其流量过程呈阶梯状且非连续性变化。类型二是根据调蓄池与被排水点之
间的水头变化进行流量调节。类型三与类型一类似，但其流量过程呈连续性变化，适用于变速水泵。
本研究涉及的三个泵站均为带有调蓄池的雨水强排泵站，因此，选择类型一中的流量与水深关系曲线
来描述水泵的启闭方式。
图 １ 不同类型水泵排水流量曲线

３ 模型求解方法

如上所述，本研究选取开源代码的 ＳＷＭＭ ［２１］ 对复杂城区水系统的水量水质动态变化过程进行模
拟。ＮＳＧＡ － Ⅱ作为一种成熟的多目标优化算法在模型参数率定、水资源调配、工程施工设计等方面得
到了广泛应用，其算法详见文献［２２］。目前，将分 布 式机 理模 型 与 遗传 优 化 算法 相结 合应 用于城
区水量水质的优化调度，在求 解过 程中面临 两个难题：一 是 在数 据 快 速交 换 中，如 何 建 立 ＳＷＭＭ
与 ＮＳＧＡ － Ⅱ之间输入输出文件的读写关系，这是两类不同方法深度耦合的第一步；二是在多线程并
行加速处理中，ＳＷＭＭ单次求解耗时长，ＮＳＧＡ － Ⅱ在优化过程中需要大种群的多次迭代寻优，如何建
立 ＳＷＭＭ与 ＮＳＧＡ － Ⅱ之间的多线程并行加速计算技术，这是解决两类方法优化求解效率的关键。
— ３ ６ １ —