Page 44 - 2023年第54卷第10期

３ 试验结果与分析

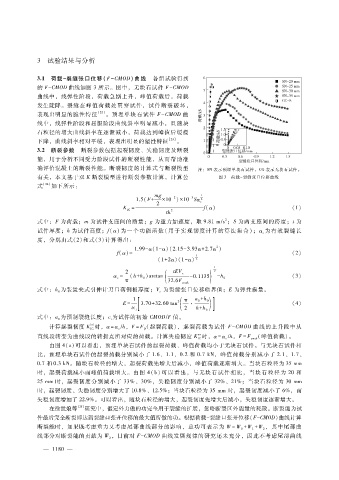
３．１ 荷载－ 裂缝张口位移（Ｆ － ＣＭＯＤ）曲线 各组试验得到
的 Ｆ － ＣＭＯＤ曲线如图 ３所示。图中，无块石试件 Ｆ － ＣＭＯＤ
曲线中，线弹性阶段，荷载急剧上升，峰值荷载后，荷载
发生陡降。裂缝在峰值荷载处贯穿试件，试件断裂破坏，
表现出明显的脆性特征 ［２２］ 。预埋单块石试件 Ｆ － ＣＭＯＤ曲
线中，线弹性阶段和屈服阶段曲线斜率明显减小，且随块
石粒径的增大曲线斜率在逐渐减小，荷载达到峰值后缓慢
下降，曲线斜率相对平缓，表现出明显的塑性特征 ［２３］ 。
３．２ 断裂参数 断裂参数包括起裂韧度、失稳韧度及断裂
能，用于分析不同受力阶段试件的断裂性能，从而帮助准
确评价混凝土的断裂性能。断裂韧度的计算式与断裂模型 注：ＳＮ表示预埋单块石试件，ＣＧ表示无块石试件。
有关，本文基于双 Ｋ断裂模型进行断裂参数计算，计算公 图 ３ 荷载－ 裂缝张口位移曲线
式 ［２４］ 如下所示：
ｍｇ １
－ ２ － ３
１ ．５（Ｆ ＋ × １０ ） × １０ Ｓ α ｃ ２
２
Ｋ ＝ ｆ（ α ） （１）
ＩＣ ２
ｔｈ
２
式中：Ｆ为荷载；ｍ为试件支座间的质量；ｇ为重力加速度，取 ９．８１ｍ?ｓ；Ｓ为两支座间的跨度；ｔ为
为有效裂缝长
试件厚度；ｈ为试件高度；ｆ（ α ）为一个功能函数（用于实现韧度计算的算法集合）；α ｃ
度，分别由式（ ２）和式（３）计算得出：
２
１ ．９９ － α （１ － α ）（２．１５ － ３．９３ α ＋ ２ ．７ α）
ｆ（ α ） ＝ （２）
３
（１ ＋ ２ α ）（１ － α ） ２
１
)
２ ｔＥＶ ｃ ２
＝ （ｈ ＋ ｈ）ａｒｃｔａｎ ( － ０ ．１１３５ － ｈ （３）
α ｃ ０ ０
π ３２．６Ｆ ｐｅａｋ
式中：ｈ为装置夹式引伸计刀口薄钢板厚度；Ｖ 为裂缝张口位移临界值；Ｅ为弹性模量。
ｃ
０
(
１
０
０
Ｅ ＝ ｔｃ[ ２ π · ａ＋ ｈ )] （４）
３．７０ ＋ ３２．６０ｔａｎ
ｈ ＋ ｈ
２
ｉ
０
式中：ａ为预制裂缝长度；ｃ为试件的初始 ＣＭＯＤ?Ｆ值。
ｉ
０
ｉｎｉ
ＩＣ
计算起裂韧度 Ｋ 时，α ＝ α ｃ ?ｈ，Ｆ ＝ Ｆ（起裂荷载），起裂荷载为试件 Ｆ － ＣＭＯＤ曲线的上升段中从
Ｑ
ｕｎ
ｐｅａｋ
直线段转变为曲线段的转折点所对应的荷载。计算失稳韧度 Ｋ 时，α ＝ α ｃ ?ｈ，Ｆ ＝ Ｆ （峰值荷载）。
ＩＣ
由图 ４（ａ）可以看出，预埋单块石试件的起裂荷载、峰值荷载均小于无块石试件。与无块石试件相
比，预埋单块石试件的起裂荷载分别减小了 １．６、１．１、０．２和 ０．７ｋＮ，峰值荷载分别减小了 ２．１、１．７、
０．７和 ０．３ｋＮ。随块石粒径的增大，起裂荷载先增大后减小，峰值荷载逐渐增大。当块石粒径为 ３５ｍｍ
时，起裂荷载减小而峰值荷载增大。由图 ４（ｂ）可以看出，与无块石试件相比，当块石粒径为 ２０和
２５ｍｍ时，起裂韧度分别减小了 ３３％、３０％，失稳韧度分别减小了 ３２％、２１％；当块石粒径为 ３０ｍｍ
时，起裂韧度、失稳韧度分别增大了 １０．８％、１２．５％；当块石粒径为 ３５ｍｍ时，起裂韧度减小了 ６％，而
失稳韧度增加了 ２２．９％。可以看出，随块石粒径的增大，起裂韧度先增大后减小，失稳韧度逐渐增大。
在徐世?等 ［２５］ 研究中，假定外力做的功完全用于裂缝的扩展，忽略断裂区外能量的耗散。断裂能为试
件最后完全断裂即达到裂缝口张开位移的最大值所做的功。根据荷载－ 裂缝口张开位移（Ｆ － ＣＭＯＤ）曲线计算
断裂能时，如果既考虑重力又考虑尾部曲线部分的影响，总功可表示为 Ｗ＝ Ｗ ＋ Ｗ ＋ Ｗ ，其中尾部曲
０ １ ２
线部分对断裂能的贡献为 Ｗ ，目前对 Ｆ － ＣＭＯＤ曲线发展规律的研究还未充分，因此不考虑尾部曲线
２
８
— １ １ ０ —