Page 79 - 2023年第54卷第10期

据处理中考虑土工织物面积计算是更严谨的选择。因此以顶压力作用下土工合成材料面积的相对变
形量作为应变，定义为 “顶压面积应变”；对应的土工织物顶破时的面积应变定义为 “顶破面积应
变”。
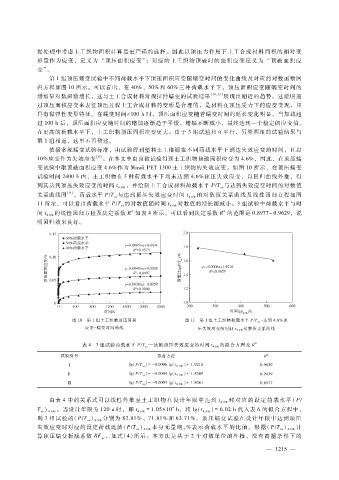
第 １组顶压蠕变试验中不同荷载水平下顶压面积应变随蠕变时间的变化曲线及对应的对数函数回
归方程如图 １０所示。可以看出，在 ４０％、５０％和 ６０％三种荷载水平下，顶压面积应变随蠕变时间的
增加呈对数函数增长，这与土工合成材料常规拉伸蠕变的试验结果 ［１０，１３］ 展现出相近的趋势。这说明通
过顶压面积应变来表征顶压过程土工合成材料的变形是合理的，是材料在顶压受力下的应变变现，且
具有黏弹性变形特征。在蠕变时间＜１００ｈ时，顶压面积应变随着蠕变时间的延长变化明显，当加载超
过 １００ｈ后，顶压面积应变随时间的增加逐渐趋于平缓，增幅不断减小，最终达到一个稳定的应变值。
在更高的荷载水平下，土工织物顶压面积应变更大。由于 ３组试验相互平行，另外两组的试验结果与
第 １组相近，这里不再赘述。
依据常规蠕变试验标准，由试验得到塑料土工格栅在不同荷载水平下到达失效应变的时间，且以
１０％应变作为失效应变 ［８］ 。在本文中由顶破试验得到土工织物顶破面积应变为 ４．６％，因此，在顶压蠕
变试验中取顶破面积应变 ４．６％作为 ＭｉｒａｆｉＰＥＴ１３００土工织物的失效应变。如图 １０所示，在顶压蠕变
试验时间 ２４００ｈ内，土工织物在 ３种荷载水平下均未达到 ４．６％顶压失效应变，以回归曲线外推，得
到其达到顶压失效应变的时间 ｔ ，并绘制土工合成材料荷载水平 Ｐ?Ｔ 与达到失效应变时间的对数值
４．６％
ａｖ
关系曲线图 ［８］ 。荷载水平 Ｐ?Ｔ 与达到顶压失效应变时间 ｔ 的对数值关系曲线及线性回归方程如图
ａｖ ４．６％
１１所示，可以看出荷载水平 Ｐ?Ｔ 的对数值随时间 ｔ 对数值的增长而减小。３组试验中荷载水平与时
４．６％
ａｖ
２
２
间 ｔ 的线性回归方程及决定系数 Ｒ 如表 ４所示，可以看到决定系数 Ｒ 的范围是 ０．８９７７～０．９６２９，说
４．６％
明回归效果良好。

图 １０ 第 １组土工织物顶压面积 图 １１ 第 １组土工织物荷载水平 Ｐ?Ｔ ａｖ 达到 ４．６％顶
－
应变－ 蠕变时间曲线 压失效应变的时间 ｔ
４．６％ 对数值关系曲线
表 ４ ３组试验荷载水平 Ｐ?Ｔ —达到顶压失效应变的时间 ｔ 的拟合方程及 Ｒ ２
ａｖ ４．６％
试验组号 拟合方程 Ｒ ２
４．６％ ） ＋１．９２１６
Ⅰ ｌｇ（Ｐ?Ｔ ａｖ ） ＝－ ０．０００６ｌｇ （ｔ ０．９６２９
４．６％ ） ＋１．８５８９
Ⅱ ｌｇ（Ｐ?Ｔ ａｖ ） ＝－ ０．０００４ｌｇ（ｔ ０．９４３９
４．６％ ） ＋１．８０６１
Ⅲ ｌｇ（Ｐ?Ｔ ａｖ ） ＝－ ０．０００３ｌｇ（ｔ ０．８９７７
由表 ４中的关系式可以线性外推至土工织物在设计年限中达到 ｔ 时对应 的设 定荷 载 水 平（Ｐ?
４．６％
６
Ｔ ） 。当设计年限为 １２０ａ时，即 ｔ ＝ １．０５ × １０ ｈ，将 ｌｇ（ｔ ） ＝６．０２ｈ 代入表 ６的拟合方程中，
４．６％
ａｖ ４．６％
４．６％
则 ３组试验的（Ｐ?Ｔ ） 分别为 ８２．８１％、７１．８１％和 ６３．７１％。顶压蠕变试验在设计年限中达到顶压
ａｖ ４．６％
失效应变时对应的设定荷载比值（Ｐ?Ｔ ） 本身无量纲，％表示荷载水平的比值。根据（Ｐ?Ｔ ） 计
ａｖ ４．６％
ａｖ ４．６％
算顶压蠕变折减系数 ＲＦ ，如式（４）所示。本方法是基于 ２个对数单位的外推，没有高温条件下的
ｐｒ
２
— １ １ ５ —