Page 81 - 2023年第54卷第10期

面积应变为 １０％时。说明顶压蠕变折减系数相对于常规拉伸蠕变折减系数的增长量较大。

表 ６ 不同设计年限及顶压面积应变下顶压蠕变相对于常规拉伸蠕变折减系数的增长幅度 γ 单位：％
试验 设计 增长幅度 γ
组号 年限?ａ Ａ ＝ １％ Ａ ＝ ２％ Ａ ＝ ３％ Ａ ＝ ４％ Ａ ＝ ４．６％ Ａ ＝ ５％ Ａ ＝ ６％ Ａ ＝ ７％ Ａ ＝ ８％ Ａ ＝ ９％ Ａ ＝ １０％
５ ９６．４１５ ９１．２６８ ８９．５４４ ８８．６８６ ８８．３４４ ８８．１７７ ８７．８２７ ８７．５７０ ８７．３９９ ８７．２５０ ８７．１３９
１０ ９３．７４３ ８８．４９９ ８６．７４３ ８５．８６９ ８５．５２１ ８５．３５１ ８４．９９５ ８４．７３３ ８４．５６０ ８４．４０８ ８４．２９４
Ⅰ
６０ ８０．７４８ ７５．４５３ ７３．６８１ ７２．８００ ７２．４４９ ７２．２７９ ７１．９２０ ７１．６５５ ７１．４８１ ７１．３２８ ７１．２１３
１２０ ７４．８３１ ６９．５５９ ６７．７９６ ６６．９１９ ６６．５６９ ６６．４００ ６６．０４４ ６５．７７９ ６５．６０７ ６５．４５５ ６５．３４０
５ １２２．５５４ １１９．１７７ １１８．０４０ １１７．４７４ １１７．２６９ １１７．１４２ １１６．９０９ １１６．７４８ １１６．６３９ １１６．５４５ １１６．４７３
１０ １１９．４３７ １１５．９５７ １１４．７８７ １１４．２０４ １１３．９９４ １１３．８６２ １１３．６２３ １１３．４５７ １１３．３４５ １１３．２４７ １１３．１７４
Ⅱ
６０ １０４．５０２ １００．８９９ ９９．６８８ ９９．０８５ ９８．８６９ ９８．７３２ ９８．４８５ ９８．３１３ ９８．１９８ ９８．０９７ ９８．０２２
１２０ ９７．７２７ ９４．１０８ ９２．８９３ ９２．２８８ ９２．０７１ ９１．９３４ ９１．６８６ ９１．５１３ ９１．３９８ ９１．２９７ ９１．２２１
５ １４８．４９６ １４６．２７２ １４５．５５０ １４５．１６４ １４５．０１６ １４４．９５８ １４４．８１１ １４４．６８９ １４４．６３１ １４４．５６８ １４４．５１０
１０ １４４．９２４ １４２．６０７ １４１．８５７ １４１．４５５ １４１．３０１ １４１．２４０ １４１．０８６ １４０．９６０ １４０．８９９ １４０．８３３ １４０．７７３
Ⅲ
６０ １２８．０３３ １２５．５７７ １２４．７８２ １２４．３５６ １２４．１９３ １２４．１２９ １２３．９６６ １２３．８３３ １２３．７６８ １２３．６９９ １２３．６３５
１２０ １２０．３９６ １１７．９１１ １１７．１０７ １１６．６７６ １１６．５１１ １１６．４４６ １１６．２８１ １１６．１４６ １１６．０８１ １１６．０１１ １１５．９４６
注：Ａ为顶压面积应变

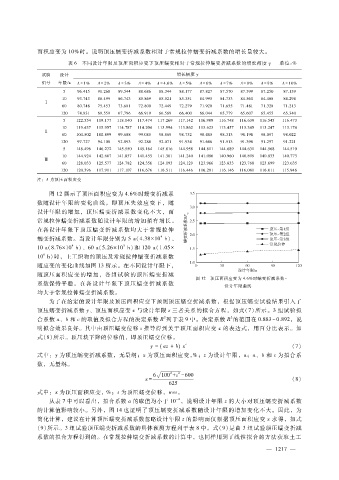
图 １２展示了顶压面积应变为 ４．６％时蠕变折减系
数随设计年限的变化曲线。即顶压 失效 应变 下，随
设计年限的增加，顶压蠕变折减系 数变化不 大，而
常规拉伸蠕变折减系数随设计年限的增加稍有增长。
在各设计年限下顶压蠕变折减系数均大于常规拉伸
４
蠕变折减系数。当设计年限分别为 ５ａ（４．３８ × １０ ｈ）、
４
５
１０ａ（８．７６ × １０ ｈ）、６０ａ（５．２６ × １０ ｈ）和 １２０ａ（１．０５ ×
６
１０ ｈ）时，土工织物的顶压及常规拉伸蠕变折减系数
随应变的变化曲线如图 １３所示。在不同设计年限下，
随顶压面积应变的增加，各组试验的顶压蠕变折 减
图 １２ 顶压面积应变为 ４．６％时蠕变折减系数－
系数保持平稳。在各设计年限下顶压蠕变折减系数
设计年限曲线
均大于常规拉伸蠕变折减系数。
为了在给定的设计年限及顶压面积应变下预测顶压蠕变折减系数，根据顶压蠕变试验结果引入了
顶压蠕变折减系数 ｙ、顶压面积应变 ｘ与设计年限 ｚ三者关系的拟合方程，如式（７）所示。３组试验拟
２
２
合系数 ａ、ｂ和 ｃ的取值及拟合方程的决定系数 Ｒ列于表 ９中。决定系数 Ｒ的范围在 ０．８８３～０．８９２，说
明拟合效果良好。其中由顶压蠕变位移 ｓ推导得到关于顶压面积应变 ｘ的表达式，用百分比表示。如
式（ ８）所示。顶压块下降的位移值，即顶压蠕变位移。
ｃ
(
ｙ ＝ ａｚ ＋ｂ ) ｘ （７）
式中：ｙ为顶压蠕变折减系数，无量纲；ｘ为顶压面积应变，％；ｚ为设计年限，ａ；ａ、ｂ和 ｃ为拟合系
数，无量纲。

２
２
６ １００＋ ｓ－ ６００
槡
ｘ ＝ （８）
６２５
式中：ｘ为顶压面积应变，％；ｓ为顶压蠕变位移，ｍｍ。
－ ４
从表 ７中可以看出，拟合系数 ａ的取值均小于 １０ ，说明设计年限 ｚ的大小对顶压蠕变折减系数
的计算值影响较小。另外，图 １４也证明了顶压蠕变折减系数随设计年限的增加变化不大。因此，为
简化计算，建议在计算顶压蠕变折减系数忽略设计年限 ｚ的影响而仅根据顶压面积应变 ｘ求得，如式
（ ９）所示。３组试验顶压蠕变折减系数的具体预测方程列于表 ８中。式（９）是由 ３组试验顶压蠕变折减
系数的拟合方程得到的。在常规拉伸蠕变折减系数的计算中，也同样用到了线性拟合的方法获取土工

２
— １ １ ７ —