Page 109 - 2024年第55卷第3期

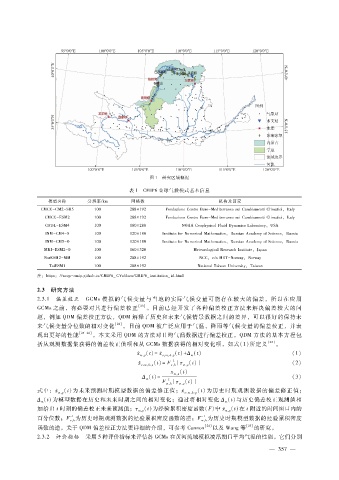
图 １ 研究区域概况

表 １ ＣＭＩＰ６全球气候模式基本信息

模型名称 分辨率?ｋｍ 网格数 机构及国家
ＣＭＣＣ － ＣＭ２ － ＳＲ５ １００ ２８８ × １９２ ＦｏｎｄａｚｉｏｎｅＣｅｎｔｒｏＥｕｒｏ － ＭｅｄｉｔｅｒｒａｎｅｏｓｕｉＣａｍｂｉａｍｅｎｔｉＣｌｉｍａｔｉｃｉ，Ｉｔａｌｙ
ＣＭＣＣ － ＥＳＭ２ １００ ２８８ × １９２ ＦｏｎｄａｚｉｏｎｅＣｅｎｔｒｏＥｕｒｏ － ＭｅｄｉｔｅｒｒａｎｅｏｓｕｉＣａｍｂｉａｍｅｎｔｉＣｌｉｍａｔｉｃｉ，Ｉｔａｌｙ
ＧＦＤＬ － ＥＳＭ４ １００ １８０ × ２８８ ＮＯＡＡＧｅｏｐｈｙｓｉｃａｌＦｌｕｉｄＤｙｎａｍｉｃｓＬａｂｏｒａｔｏｒｙ，ＵＳＡ
ＩＮＭ－ ＣＭ４ － ８ １００ １２０ × １８０ ＩｎｓｔｉｔｕｔｅｆｏｒＮｕｍｅｒｉｃａｌＭａｔｈｅｍａｔｉｃｓ ，ＲｕｓｓｉａｎＡｃａｄｅｍｙｏｆＳｃｉｅｎｃｅ，Ｒｕｓｓｉａ
ＩＮＭ－ ＣＭ５ － ０ １００ １２０ × １８０ ＩｎｓｔｉｔｕｔｅｆｏｒＮｕｍｅｒｉｃａｌＭａｔｈｅｍａｔｉｃｓ，ＲｕｓｓｉａｎＡｃａｄｅｍｙｏｆＳｃｉｅｎｃｅ，Ｒｕｓｓｉａ
ＭＲＩ － ＥＳＭ２ － ０ １００ １６０ × ３２０ ＭｅｔｅｏｒｏｌｏｇｉｃａｌＲｅｓｅａｒｃｈＩｎｓｔｉｔｕｔｅ ，Ｊａｐａｎ
ＮｏｒＥＳＭ２ － ＭＭ １００ ２８８ × １９２ ＮＣＣ ，ｃ?ｏＭＥＴ － Ｎｏｒｗａｙ，Ｎｏｒｗａｙ
ＴａｉＥＳＭ１ １００ ２８８ × １９２ ＮａｔｉｏｎａｌＴａｉｗａｎＵｎｉｖｅｒｓｉｔｙ，Ｔａｉｗａｎ
注：ｈｔｔｐｓ：??ｗｃｒｐ － ｃｍｉｐ．ｇｉｔｈｕｂ．ｉｏ?ＣＭＩＰ６＿ＣＶｓ?ｄｏｃｓ?ＣＭＩＰ６＿ｉｎｓｔｉｔｕｔｉｏｎ＿ｉｄ．ｈｔｍｌ

２．３ 研究方法
２．３．１ 偏差校正 ＧＣＭｓ模拟的气候变量与当地的实际气候变量可能存在较大的偏差，所以在应用
ＧＣＭｓ之前，有必要对其进行偏差校正 ［２３］ 。目前已经开发了各种偏差校正方法来解决偏差较大的问
题，例如 ＱＤＭ偏差校正方法，ＱＤＭ解释了历史和未来气候情景数据之间的差异，可以很好的保持未
来气候变量分位数的相对变化 ［２４］ 。目前 ＱＤＭ被广泛应用于气温、降雨等气候变量的偏差校正，并表
现出更好的性能 ［２５ － ２６］ 。本文采用 ＱＤＭ的方法对日均气温数据进行偏差校正。ＱＤＭ方法的基本方程包
括从观测数据集获得的偏差校正值项和从 ＧＣＭｓ数据获得的相对变化项，如式（１）所定义 ［２３］ 。
＾ （ｔ） ＝＾ （ｔ） ＋ Δ ｍ （ｔ） （１）
ｘ
ｘ
ｍ，ｐ ｏ：ｍ，ｈ：ｐ
－ １
＾
ｘ ｏ：ｍ，ｈ：ｐ （ｔ） ＝Ｆ ［ τ ｍ，ｐ （ｔ）］ （２）
ｏ，ｈ
ｘ （ｔ）
ｍ，ｐ
（ｔ） ＝ （３）
Δ ｍ
－ １
ｍ，ｈ
Ｆ ［ τ ｍ，ｐ （ｔ）］
式中： ＾ｘ （ｔ）为未来预测时期模型数据的偏差修正值； ＾ｘ （ｔ）为历史时期观测数据的偏差修正值；
ｍ，ｐ
ｏ：ｍ，ｈ：ｐ
（ｔ）与历史偏差校正观测值相
Δ ｍ （ｔ）为模型数据在历史和未来时期之间的相对变化；通过将相对变化 Δ ｍ
（ｔ）为经验累积密度函数（Ｆ）中 ＾ｘ （ｔ）在 ｔ附近的时间窗口内的
ｍ，ｐ
加给出 ｔ时刻的偏差校正未来预测值；τ ｍ，ｐ
－ １
－ １
百分位数；Ｆ 为历史时期观测数据的经验累积密度函数的逆；Ｆ 为历史时期模型数据的经验累积密度
ｏ，ｈ ｍ，ｈ
［２４］
函数的逆。关于 ＱＤＭ偏差校正方法更详细的介绍，可参考 Ｃａｎｎｏｎ 以及 Ｗａｎｇ等 ［２３］ 的研究。
２．３．２ 评价指标 采用 ５种评价指标来评估各 ＧＣＭｓ在黄河流域模拟凌汛期日平均气温的性能。它们分别
— ３ ５ ７ —