Page 90 - 2021年第52卷第7期

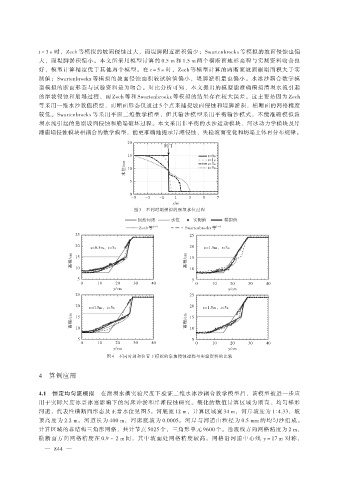
t = 3 s 时，Zech 等模拟的坡面侵蚀过大，而堤脚附近淤积偏少；Swartenbroekx 等模拟的坡面侵蚀也偏
大，而堤脚淤积偏小。本文所采用模型计算的 0.5 m 和 1.5 m 两个横断面地形高程与实测资料吻合良
好，模型计算精度优于其他两个模型。在 t = 5 s 时，Zech 等模型计算的两断面坡面崩塌面积大于实
测值；Swartenbroekx 等模拟的坡面侵蚀面积较试验值偏小，堤脚淤积量也偏小。水冰沙耦合数学模
型模拟的断面形态与试验资料最为吻合。对比分析可知，本文提出的模型能准确模拟溃坝水流引起

的岸坡侵蚀和崩塌过程，而 Zech 等和 Swartenbroekx 等模拟的结果存在较大误差。这主要是因为 Zech
等采用一维水沙数值模型，而断面形态仅通过 5 个点来捕捉坡面侵蚀和堤脚淤积，横断面的网格精度
较低。Swartenbroekx 等采用平面二维数学模型，但其输沙模型采用平衡输沙模式，不能准确模拟溃
坝水流引起的急剧坡面侵蚀和崩塌破坏过程。本文采用非平衡的水沙运动模块、河冰动力学模块及岸
滩崩塌侵蚀模块相耦合的数学模型，能更准确地揭示岸滩侵蚀、失稳坡面变化和坍塌土体再分布规律。

20
闸门
15 t=0s
t=1s
水位/cm 10 t=5s
t=3s

5
0
-5 -3 -1 1 3 5 7
x/m
图 3 不同时刻模拟的溃坝水位过程
初始河床 水位 实测值 模拟值
Zech等 ［19］ Swartenbroekx等 ［31］
25 25

20 20
x=0.5m，t=3s x=1.5m，t=3s
高程/cm 15 高程/cm 15
10
10
5 5
0 10 20 30 40 0 10 20 30 40
y/cm y/cm
25 25

20 20
x=0.5m，t=5s x=1.5m，t=5s
高程/cm 15 高程/cm 15

10
10
5 5
0 10 20 30 40 0 10 20 30 40
y/cm y/cm
图 4 不同时刻和位置下模拟的岸坡侵蚀过程与实验资料的比较

4 算例应用

4.1 恒定均匀流模拟 在溃坝水槽实验尺度下验证二维水冰沙耦合数学模型后，该模型被进一步应

用于实际尺度冰盖冰塞影响下的河床冲淤和岸滩侵蚀研究。概化的数值计算区域为顺直、均匀梯形
河道，代表性横断面形态及正常水位见图 5。河底宽 12 m，计算区域宽 34 m，河岸坡度为 1∶4.33，坡
顶高度为 2.2 m。河道长为 400 m，河床底坡为 0.0005。河岸与河道由粒径为 0.5 mm 的均匀沙组成。
计算区域的非结构三角形网格，共计节点 5025 个，三角形单元 9600 个。沿流线方向网格精度为 2 m，
横断面方向网格精度在 0.9 ~ 2 m 间，其中坡面处网格精度较高。网格沿河道中心线 y = 17 m 对称，

— 844 —