Page 10 - 2023年第54卷第4期

为考虑了扬压力上托作用之后的坝－ 基交界面下侧的应力，即交界面处的有效应力。
竖向应力 σ ｕ 、σ ｄ
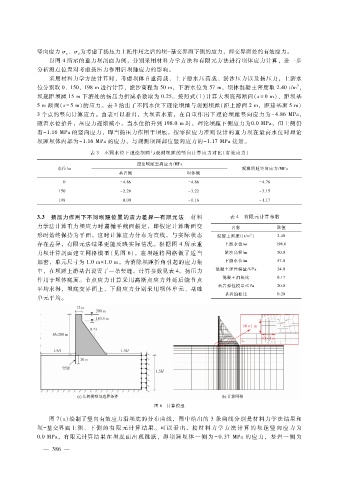
以图 ４所示的重力坝剖面为例，分别采用材料力学方法和有限元方法进行坝体应力计算，进一步
分析测点位置对考虑扬压力作用后坝踵应力的影响。
采用材料力学方法计算时，考虑坝体自重荷载、上下游水压荷载、淤沙压力以及扬压力，上游水
３
位分别取 ０、１５０、１９８ｍ进行计算，淤沙高程为 ５０ｍ，下游水位为 ５７ｍ，坝体混凝土密度取 ２．４０ｔ?ｍ ，
坝底距坝踵 １５ｍ下游处的扬压力折减系数取为 ０．２５。按照式（１）计算大坝底部断面（ｚ ＝ ０ｍ ）、距坝基
５ｍ断面（ｚ ＝ ５ｍ ）的应力。表 ３给出了不同水位下理论坝踵与观测坝踵（距上游面 ２ｍ，距建基面 ５ｍ）
３个点的竖向计算应力。由表可以看出，大坝蓄水前，在自重作用下理论坝踵竖向应力为 － ４．８６ＭＰａ ，
随着水位抬升，压应力逐渐减小，当水位抬升到 １９８．０ｍ时，理论坝踵下侧应力为０．０ＭＰａ，但上侧仍
有－ １．１６ＭＰａ的竖向应力，即当扬压力作用于坝底，按零拉应力准则设计的重力坝在最高水位时理论
坝踵坝体内部为－ １．１６ＭＰａ 的应力，与观测坝踵部位竖向应力的－ １．１７ＭＰａ 接近。

表 ３ 不同水位下理论坝踵与观测坝踵的竖向计算应力对比（有效应力）

理论坝踵竖向应力?ＭＰａ
水位?ｍ 观测坝踵竖向应力?ＭＰａ
基岩侧 坝体侧
０ － ４．８６ － ４．８６ － ４．７６
１５０ － ２．２６ － ３．２２ － ３．１５
１９８ ０．００ － １．１６ － １．１７

３．３ 扬压力作用下不同坝踵位置的应力差异—有限元法 材料 表 ４ 有限元计算参数
力学法计算重力坝应力时遵循平截面假定，即假定计算断面变 名称 取值
形时始终保持为平面，这时计算应力分布为直线，与实际状态 混凝土密度?（ｔ?ｍ ） ２．４０
３
存在差异，有限元法结果更能反映实际情况。根据图 ４所示重 上游水位?ｍ １９８．０
力坝计算剖面建立网格模型（见图 ６），在坝踵将网格做了适当 淤沙高程?ｍ ５０．０
加密，单元尺寸为 １．０ｍ × １．０ｍ。为消除坝踵折角引起的应力集 下游水位?ｍ ５７．０
中，在坝踵上游基岩设置了一条竖缝。计算参数见表 ４。扬压力 混凝土弹性模量?ＧＰａ ２４．０
混凝土泊松比 ０．１７
作用于坝体底面。节点应力计算采用高斯点应力外延后绕节点
基岩弹性模量?ＧＰａ ２０．０
平均求得，坝底交界面上、下侧应力分别采用坝体单元、基础
基岩泊松比 ０．２０
单元平均。

图 ６ 计算模型

图 ７（ａ）绘制了竖向有效应力沿坝底的分布曲线，图中给出的 ３条曲线分别是材料力学法结果和
坝－ 基交界面 上 测、下 侧 的 有 限 元 计 算 结 果。可 以 看 出，按 材 料 力 学 方 法 计 算 的 坝 踵 竖 向 应 力 为
０．０ＭＰａ，有限元计算结果 在坝底 面出 现跳 跃，即坝踵坝 体 一 侧 为 － ０．３７ＭＰａ的 应 力，基 岩 一 侧 为

６
— ３ ８ —