Page 11 - 2023年第54卷第4期

２．０８ＭＰａ的拉应力。除坝踵、坝趾部位外，基岩一侧材料力学法与有限元法计算应力基本相同。由于
扬压力作用在坝底面，对坝体有 “上托” 作用，从而在基岩一侧产生拉应力增量，在坝体一侧产生压
应力增量，两者从上游到下游普遍存在一个应力差，坝踵部位相差 ２．４５ＭＰａ，形成了基岩一侧为拉、
坝体一侧为压的应力分布。
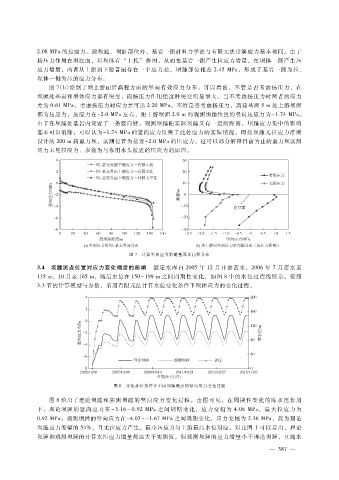
图 ７（ｂ）绘制了坝上游面沿高程方向的竖向有效应力分布。可以看出，不管是否考虑扬压力，在
坝踵处基岩和坝体应力都有突变，而扬压力作用使这种突变明显增大。当不考虑扬压力时两者的应力
差为 ０．６１ＭＰａ，考虑扬压力时应力差可达 ２．２０ＭＰａ。不管是否考虑扬压力，离建基面 ５ｍ处上游坝面
都为压应力，压应力在－ ２．０ＭＰａ 左右，距上游坝面 ２．０ｍ的观测坝踵位置的竖向压应力为－ １．７４ＭＰａ 。
由于在坝踵处基岩内设置了一条竖向缝，观测坝踵距实际坝踵又有一定的距离，坝踵应力集中的影响
基本可以消除，可以认为－ １．７４ＭＰａ的竖向应力反映了此处应力的实际情况，即按坝踵无拉应力准则
设计的 ２００ｍ高重力坝，实测位置为接近－ ２．０ＭＰａ 的压应力。这可以部分解释目前为止的重力坝实测
应力未见拉应力、多数为与作用水头接近的压应力的原因。

图 ７ 计算竖向应力沿建基面及高程分布

３．４ 坝踵测点位置对应力变化幅度的影响 假定水库自 ２００５年 １２月开始蓄水，２００６年 ７月蓄水至
１３５ｍ，１０月至 １６５ｍ，随后水位在 １５０～１９８ｍ之间周期性变化，如图 ８中的水位过程线所示。按照
３．３节的计算模型与参数，采用有限元法计算水位变化条件下坝体应力的变化过程。

图 ８ 变化水位条件下不同坝踵测点的竖向应力变化过程

图 ８给出了理论坝踵和实测坝踵的竖向应力变化过程。由图可见，在周期性变化的库水压作用
下，理论坝踵的竖向应力在 － ３．１６～０．９２ＭＰａ 之间周期变化，应力变幅为 ４．０８ＭＰａ，最大拉应力为
０．９２ＭＰａ；观测坝踵的竖向应力在－ ４．０３～ － １．６７ＭＰａ 之间周期变化，应力变幅为 ２．３６ＭＰａ，仅为理论
坝踵应力变幅的 ５４％，且无拉应力产生，最小压应力与上游最高水位对应。对比图 １可以看出，理论
坝踵和观测坝踵的计算水压应力增量都远大于实测值，但观测坝踵的应力增量小于理论坝踵，且随水

— ３ ８ ７ —