Page 20 - 2023年第54卷第10期
P. 20
X = XCauchy( α ) (8)
i(new) i
根据柯西累积分布公式,即公式( 9),最优个体柯西变异数学模型为:
F(x)= π ( - 1 ) arctan(x) + 0.5 (9)
X i(new) = X(1 + tan( π (r -0.5 ))) (10)
i
式中:X 为柯西变异后的最优个体位置;X为变异前最优个体位置;r为(0,1)间的随机数。
i(new) i
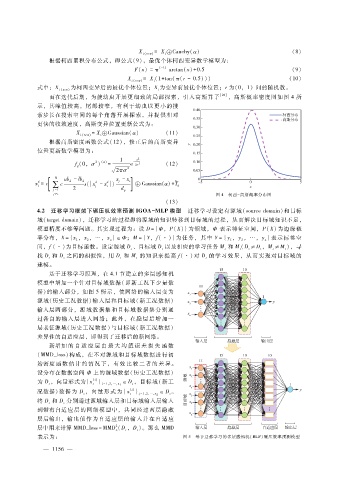
而在迭代后期,为使幼虫开展更细致的局部探索,引入高斯算子 [26] ,高斯概率密度图如图 4所
示,其峰值较高,尾部较窄,有利于幼虫以更小的搜
索步长在搜索空间的每个角落开展探索,并提供相对
更快的收敛速度,高斯变异位置更新公式为:
X i(new) =XGaussian( α ) (11)
i
根据高斯密度函数公式(12),修正后的高斯变异
位置更新数学模型为:
1 - α 2
2 ( α )
f(0,σ) = e 2 σ 2 (12)
g 2
槡 2 πσ
^
i
d
d
j
d
d
d
x=c ∑ [ N c ub - lb s(x - x ) x- x ] Gaussian( α ) + T
i
d
j
i
j = 1 2 d ij
j ≠i 图 4 柯西- 高斯概率分布图
(13)
4.2 迁移学习框架下碾压机效率预测 IGOA - MLP模型 迁移学习设定有源域(sourcedomain)和目标
域(targetdomain),迁移学习的过程即将源域的知识转移到目标域的过程,从而解决目标域知识不足,
模型精度不够等问题。其实现过程为:设 D = { Φ,P(X)}为领域,Φ 表示特征空间,P(X)为边缘概
率分布,X = {x,x,…,x} ∈Φ;M= {Y,f(·)}为任务,其中 Y = {y,y,…,y}表示标签空
n
1
2
n
2
1
间,f(·)为目标函数。设定源域 D、目标域 D 以及相应的学习任务 M 和 M(D≠D,M ≠M),寻
s t s t s t s t
找 D 和 D 之间的相似性,用 D 和 M 的知识来提高 f(·)对 D 的学习效果,从而实现对目标域的
s t s s t
建模。
基于迁移学习原理,在 4.1节建立的多层感知机
模型中增加一个针对目标域数据(即新工况下少量数
据)的输入部分,如图 5所示,使网络的输入层变为
源域(历史工况数据)输入层和目标域(新工况数据)
输入层两部分,源域数据集和目标域数据集分别通
过各自的输入层进入网络;此外,在隐层 后增 加一
层表征源域(历史工况数据)与目标域(新工况数据)
差异性的自适应层,即得到了迁移后的新网络。
新增加 的 自 适 应 层 由 最 大 均 值 误 差 损 失 函 数
( MMD_loss)构成,在不对源域和目标域数据进行初 15
始密度 函 数 估 计 的 情 况 下,有 效 比 较 二 者 的 差 异。
设分布在数据空间 Φ 上的源域数据(历史工况数据)
(i)
为 D,向量形式为{x } ∈D,目标域(新工
s s i = 1 ,2,…,n 1 s
(j)
况数据)数据为 D,向 量形 式为 {x } ∈ D。
t t j = 1,2,…,n 2 t
将 D 和 D 分别通过源域输入层和目标域输入层输入
t
s
到带有自适应层的网络模型中,共同经过两层隐藏 ·
· ·
层后输出,输出值作为自适应层的输入并在自适 应
2
层中用来计算 MMD_loss = MMD(D,D)。那么 MMD 隐藏层
a s t
表示为: 图 5 基于迁移学习的多层感知机(MLP)碾压效率预测模型
5
— 1 1 6 —