Page 23 - 2023年第54卷第10期

折均值分别为 ０．５３２、１．００６、０．９９１、０．２０３，均小于其他模型，表明本文所选取的 ＭＬＰ模型在处理碾
压效率这一仿真参数的预测问题时预测精度最高，拟合效果最好，同时，模型指标五折标准差也在可
接受范围内。因此，ＭＬＰ模型能够用于高心墙堆石坝施工仿真参数预测研究。

表 ４ 不同基础模型预测性能评价指标均值对比分析
评价指标 ＢＰＮＮ ＳＶＲ ＸＧＢｏｏｓｔ ＲＦ ＧＢＤＴ ＭＬＰ ＥＬＭ

ＭＡＥ ０．８３４ ０．５４９ ０．８５８ ０．６２７ １．０３０ ０．５３２ １．３２２
ＭＳＥ １．３６４ １．１４０ １．１８４ １．０９２ １．５３７ １．００６ ２．３２３
ＲＭＳＥ １．１６７ １．０６８ １．０８８ １．０４５ １．２４０ ０．９９１ １．５２４

ＭＡＰＥ ０．９１９ ０．８７６ ０．７２８ ０．６５６ １．０３３ ０．２０３ １．１１５

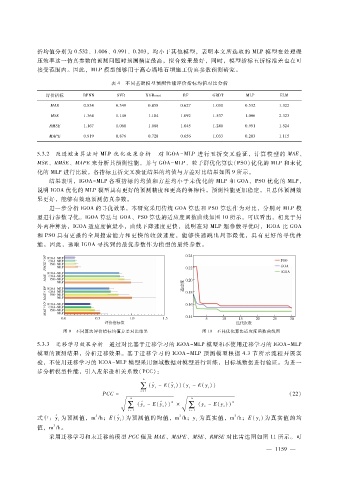
５．３．２ 改进蝗虫算法对 ＭＬＰ优化效 果分 析 对 ＩＧＯＡ － ＭＬＰ进 行 五 折交 叉验 证，计 算 模 型的 ＭＡＥ、
ＭＳＥ、ＲＭＳＥ、ＭＡＰＥ来分析其预测性能，并与 ＧＯＡ － ＭＬＰ、粒子群优化算法（ＰＳＯ）优化的 ＭＬＰ和未优
化的 ＭＬＰ进行比较。各指标五折交叉验证结果的均值与方差对比结果如图 ９所示。
结果表明，ＩＧＯＡ － ＭＬＰ各项指标的均值和方差均小于未优化的 ＭＬＰ和 ＧＯＡ、ＰＳＯ优化的 ＭＬＰ，
说明 ＩＧＯＡ优化的 ＭＬＰ模型具有更好的预测精度和更高的鲁棒性，预测性能更加稳定，且总体预测效
果更好，能够有效地预测仿真参数。
进一步分析 ＩＧＯＡ的寻优效果，本研究采用传统 ＧＯＡ算法和 ＰＳＯ算法作为对比，分别对 ＭＬＰ模
型进行参数寻优。ＩＧＯＡ算法与 ＧＯＡ、ＰＳＯ算法的适应度函数曲线如图 １０所示。可以看出，相比于另
外两种算法，ＩＧＯＡ适应度值最小，曲线下降速度更快，说明在对 ＭＬＰ超参数寻优时，ＩＧＯＡ比 ＧＯＡ
和 ＰＳＯ具有更强的全局搜索能力和 更快 的 收敛速 度，能够 快速 跳出 局 部 最优，具 有 更 好的寻优性
能。因此，选取 ＩＧＯＡ寻找到的最优参数作为模型的最终参数。

图 ９ 不同算法评价指标均值方差对比结果 图 １０ 不同优化算法适应度函数曲线图

５．３．３ 迁移学习效果分析 通过对比基于迁移学习的 ＩＧＯＡ － ＭＬＰ模型和不使用迁移学习的 ＩＧＯＡ － ＭＬＰ
模型的预测结果，分析迁移效果。基于迁移学习的 ＩＧＯＡ － ＭＬＰ预测模型根据 ４．３节所示流程开展实
验，不使用迁移学习的 ＩＧＯＡ － ＭＬＰ模型采用源域数据对模型进行训练，目标域数据进行验证。为进一
步分析模型性能，引入皮尔逊相关系数（ ＰＣＣ）：
ｎ
＾
＾
∑ （ ｙ －Ｅ （ ｙ ））（ｙ －Ｅ （ｙ））
ｉ
ｉ
ｉ
ｉ
ｉ ＝１
ＰＣＣ＝ （２２）
ｎ ＾ ＾ ２ ｎ ２
∑
∑
槡 （ ｙ －Ｅ（ ｙ ）） × 槡 （ｙ －Ｅ（ｙ））
ｉ
ｉ
ｉ
ｉ
ｉ ＝１
ｉ ＝１
＾
＾
３
３
３
式中：ｙ为预测值，ｍ ?ｈ；Ｅ（ｙ）为预测值的均值，ｍ ?ｈ；ｙ为真实值，ｍ ?ｈ；Ｅ（ｙ）为真实值的均
ｉ
ｉ
ｉ
ｉ
３
值，ｍ ?ｈ。
采用迁移学习和未迁移的模型 ＰＣＣ值及 ＭＡＥ、ＭＡＰＥ、ＭＳＥ、ＲＭＳＥ对比雷达图如图 １１所示。可
１
— １ ５ ９ —