Page 19 - 2023年第54卷第10期

针对 ＭＬＰ模型的超参数设置问题，本文采用
ＩＧＯＡ优化 ＭＬＰ的超参数。蝗虫优化算法（Ｇｒａｓｓｈｏｐｐｅｒ
ＯｐｔｉｍｉｚａｔｉｏｎＡｌｇｏｒｉｔｈｍ ， ＧＯＡ）是 Ｍｉｒｊａｌｉｌｉ等 人 在
２０１７年提出的一种新型群智能算法，通过模拟蝗
虫群体捕食行为迭代搜索最优解，其中蝗虫成虫
在前期进行全局搜索，蝗虫幼虫负责在后期对特
定临近区域进行细致开发，第 ｉ个蝗虫在第 ｄ维
的位置模型为 ［２５］ ：
ｉ
＾
ｊ
ｄ
ｄ
ｄ
ｄ
ｘ ＝ｃ ∑ [ Ｎ ｃ ｕｂ －ｌｂ ｄ ｓ（ ｘ －ｘ ） ｘ －ｘ ] ＋Ｔ
ｉ ｊ ｉ ｄ
ｊ ＝１ ２ ｄ ｉｊ
ｊ ≠ｉ
图 ２ 多层感知机（ＭＬＰ）基础模型网络结构图
（５）
ｄ
ｄ
式中：角标 ｄ表示在第 ｄ维空间；ｕｂ、ｌｂ 分别表示蝗虫搜索的上界和下界； ｘ － ｘ 为第 ｉ只蝗虫到
ｊ
ｉ
ｄ
ｄ
＾
第 ｊ只蝗虫的欧几里得距离； ｘ － ｘ ?ｄ为第 ｉ只到第 ｊ只蝗虫的单位向量；Ｔ 表示到目前为止蝗虫群
ｊ ｉ ｉｊ ｄ
体搜索的目标位置（最优值）；ｓ（ｚ）为表征群体社交作用力范围和强弱的因子；ｃ为控制参数（线性缩减
因子）：
ｃ － ｃ
ｍａｘ
ｍｉｎ
ｃ ＝ ｃ － ｔ （６）
ｍａｘ
Ｔ ｍａｘ
式中：ｔ为迭代次数；Ｔ 为最大迭代次数；ｃ 和 ｃ 为缩减因子 ｃ的上下界，本文设定 ｃ ＝ ２ ，ｃ ＝ ０ 。
ｍａｘ ｍａｘ ｍｉｎ ｍａｘ ｍｉｎ
通过式（ ５）可以看出，控制参数 ｃ影响着整个寻优过程，公式内层 ｃ用来控制蝗虫群体的交互空
间，减小排斥与吸引空间，外层 ｃ为比例因子，用来缩小搜索范围。在基本 ＧＯＡ中，ｃ为由 ２到 ０的
线性缩减过程，前期和后期下降过快，易在早期和末期陷入局部最优，中期下降慢则影响搜索速度，
难以充分体现蝗虫群体的搜索特点。为了实现对蝗虫群体的动态调节，本研究采用控制参数自适应更
新策略重构函数 ｃ（ｔ）：
２
ｔ
π
{ [ ( ) ]}
ｃ ＝ （ｃ － ｃ ） × １ － ｓｉｎ · （７）
ｍｉｎ
ｍａｘ
Ｔ
ｍａｘ ２
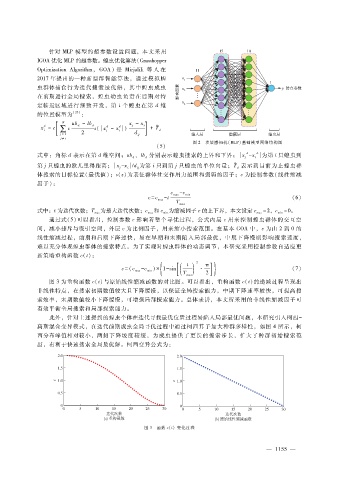
图 ３为重构函数 ｃ（ｔ）与原始线性缩减函数的对比图。可以看出，重构函数 ｃ（ｔ）的递减过程呈现出
非线性特点，在搜索初期数值较大且下降缓慢，以保证全局搜索能力，中期下降速率较快，可提高搜
索效率，末期数值较小下降缓慢，可增强局部探索能力。总体来讲，本文所采用的非线性缩减因子可
有效平衡全局搜索和局部探索能力。
此外，针对上述提到的蝗虫个体在迭代寻找最优位置过程易陷入局部最优问题，本研究引入柯西－
高斯混合变异模式，在迭代前期成虫全局寻优过程中通过柯西算子加大种群多样性，如图 ４所示，柯
西分布峰值相对较小，两侧下降坡度较缓，为成虫提供了更长的搜索步长，扩大了种群初始搜索范
围，有利于快速搜索全局最优解。柯西变异公式为：

图 ３ 函数 ｃ（ｔ）变化过程

１
— １ ５ ５ —