Page 65 - 2023年第54卷第10期

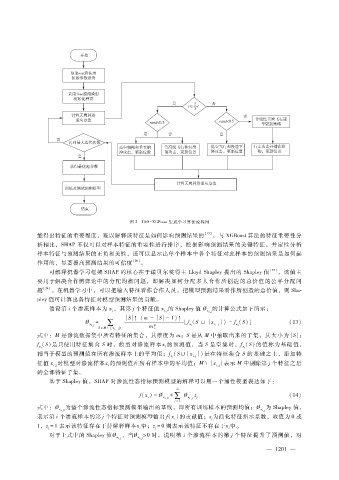
图 ２ ＩＡＯ － ＸＧＢｏｏｓｔ集成学习算法流程图

能得出特征的重要程度，难以解释该特征是如何影响预测结果的 ［１７］ 。与 ＸＧＢｏｏｓｔ算法的特征重要性分
析相比，ＳＨＡＰ不仅可以对样本特征的重要性进行排序，挖掘影响预测结果的关键特征，并定性分析
样本特征与预测结果的正负相关性，还可以显示出单个样本中各个特征对此样本的预测结果是如何起
作用的，显著提高预测结果的可信度 ［２０］ 。
可解释机器学习框架 ＳＨＡＰ的核心在于诺贝尔奖得主 ＬｌｏｙｄＳｈａｐｌｅｙ提出的 Ｓｈａｐｌｅｙ值 ［３３］ ，该值主
要用于解决合作博弈论中的分配均衡问题，即解决如何分配多人合作所创造的总价值的公平分配问
题 ［３４］ 。在机器学习中，可以把输入特征看作合作人员，把模型预测结果看作所创造的总价值，则 Ｓｈａ
ｐｌｅｙ值可计算出各特征对模型预测结果的贡献。
假设第 ｉ个渗流样本为 ｘ，其第 ｊ个特征值 ｘ 的 Ｓｈａｐｌｅｙ值  的计算公式如下所示：
ｉ ｉ，ｊ ｘ ｉ，ｊ
Ｓ！（ｍ － Ｓ －１）！
 ＝ ∑ ［ｆ（Ｓ ∪ ｛ｘ ｝）－ｆ（Ｓ）］ （１３）
ｘ ｉ，ｊ ｘ ｉ ｉ，ｊ ｘ ｉ
{
Ｓ ∈Ｍ＼ ｘ ｉ，ｊ } ｍ！
式中：Ｍ是渗流数据集中所有特征的集合，其维度为 ｍ；Ｓ是从 Ｍ中抽取出来的子集，其大小为 Ｓ；
ｆ（Ｓ）是只使用特征集合 Ｓ时，模型对渗流样本ｘ的预测值，当 Ｓ是空集时，ｆ（Ｓ）的值称为基础值，
ｘ ｉ ｉ ｘ ｉ
相当于模型的预测值在所有渗流样本上的平均值；ｆ（Ｓ ∪｛ｘ ｝）是在特征集合 Ｓ的基础之上，添加特
ｘ ｉ ｉ，ｊ
征值 ｘ 时模型对渗流样本ｘ的预测值在所有样本中的平均值；Ｍ＼｛ｘ ｝表示 Ｍ中剔除第 ｊ个特征之后
ｉ
ｉ，ｊ
ｉ，ｊ
的全部特征子集。
基于 Ｓｈａｐｌｅｙ值，ＳＨＡＰ对渗流性态指标预测模型的解释可以用一个加性模型表达如下：
ｍ
＋
ｆ（ｘ） ＝ ｘ ｉ，０ ∑  ｚ （１４）
ｉ
ｘ ｉ，ｊ ｊ
ｊ ＝１
式中： 为整个渗流性态指标预测模型输出的基线，即所有训练样本的预测均值； 为 Ｓｈａｐｌｅｙ值，
ｘ ｉ，０ ｘ ｉ，ｊ
表示第 ｉ个渗流样本的第 ｊ个特征对预测模型输出 ｆ（ｘ）的贡献值；ｚ为简化特征指示系数，取值为 ０或
ｉ ｊ
１，ｚ ＝ １ 表示该特征存在于待解释样本ｘ中；ｚ ＝ ０ 则表示该特征不存在于ｘ中。
ｊ
ｊ
ｉ
ｉ
对于上式中的 Ｓｈａｐｌｅｙ值 ，当 ＞０时，说明第 ｉ个渗流样本的第 ｊ个特征提升了预测值，对
ｘ ｉ，ｊ ｘ ｉ，ｊ
２
— １ ０ １ —