Page 68 - 2023年第54卷第10期

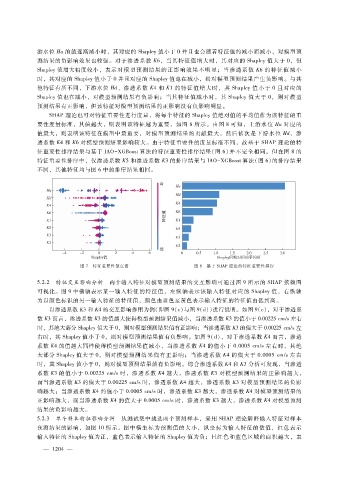
游水位 Ｈｕ的值逐渐减小时，其对应的 Ｓｈａｐｌｅｙ值小于 ０并且也会随着特征值的减小而减小，对模型预
测结果的负影响效果也较强。对于渗透系数 Ｋ６，当其特征值增大时，其对应的 Ｓｈａｐｌｅｙ值大于 ０，但
Ｓｈａｐｌｅｙ值增大幅度较小，表示对模型预测结果的正影响效果不明显；当渗透系数 Ｋ６的特征值减小
时，其对应的 Ｓｈａｐｌｅｙ值小于 ０并且对应的 Ｓｈａｐｌｅｙ值也在减小，则对模型预测结果产生负影响。与其
他特征有所不同，下游水位 Ｈｄ、渗透系数 Ｋ４和 Ｋ１的特征值增大时，其 Ｓｈａｐｌｅｙ值小于 ０且对应的
Ｓｈａｐｌｅｙ值也在减小，对模型预测结果有负影响；当其特征值减小时，其 Ｓｈａｐｌｅｙ值大于 ０，则对模型
预测结果有正影响，但该特征对模型预测结果的正影响没有负影响明显。
ＳＨＡＰ理论也可对特征重要性进行度量，将每个特征的 Ｓｈａｐｌｅｙ值绝对值的平均值作为该特征的重
要性度量标准，其值越大，则表明该特征越为重要，如图 ８所示。由图 ８可知，上游水位 Ｈｕ对应的
值最大，则表明该特征在模型中最重要，对模型预测结果的贡献最大，然后依次是下游水位 Ｈｄ、渗
透系数 Ｋ４和 Ｋ６对模型预测结果影响较大。由于特征重要性的度量标准不同，故基于 ＳＨＡＰ理论的特
征重要性排序结果与基于 ＩＡＯ － ＸＧＢｏｏｓｔ算法的特征重要性排序结果（图 ６）并不完全相同。但在图 ８的
特征重要性排序中，仅渗透系数 Ｋ５和渗透系数 Ｋ３的排序结果与 ＩＡＯ － ＸＧＢｏｏｓｔ算法（图 ６）的排序结果
不同，其他特征均与图 ６中的排序结果相同。

图 ７ 特征重要性散点图 图 ８ 基于 ＳＨＡＰ理论的特征重要性排序

５．２．２ 特征交互影响分析 两个输入特征对模型预测结果的交互影响可通过图 ９所示的 ＳＨＡＰ依赖图
可视化。图 ９中横轴表示某一输入特征的特征值，左纵轴表示该输入特征对应的 Ｓｈａｐｌｅｙ值，右纵轴
为以颜色标识的另一输入特征的特征值，颜色由蓝色至黄色表示输入特征的特征值由低到高。
以渗透系数 Ｋ３和 Ｋ４的交互影响作用为例（即图 ９（ｃ）与图 ９（ｄ））进行说明。如图 ９（ｃ），对于渗透系
数 Ｋ３而言，渗透系数 Ｋ３的值越大使得模型预测结果值减小，当渗透系数 Ｋ３的值小于 ０．００２２５ｃｍ?ｓ左右
时，其绝大部分 Ｓｈａｐｌｅｙ值大于 ０，则对模型预测结果值有正影响；当渗透系数 Ｋ３的值大于 ０．００２２５ｃｍ?ｓ左
右时，其 Ｓｈａｐｌｅｙ值小于 ０，则对模型预测结果值有负影响。如图 ９（ｄ），对于渗透系数 Ｋ４而言，渗透
系数 Ｋ４的值越大同样使得模型预测结果值减小，当渗透系数 Ｋ４的值小于 ０．０００５ｃｍ?ｓ左右时，其绝
大部分 Ｓｈａｐｌｅｙ值大于 ０，则对模型预测结果值有正影响；当渗透系数 Ｋ４的值大于 ０．０００５ｃｍ?ｓ左右
时，其 Ｓｈａｐｌｅｙ值小于 ０，则对模型预测结果值有负影响。综合渗透系数 Ｋ４和 Ｋ３分析可发现，当渗透
系数 Ｋ３的值小于 ０．００２２５ｃｍ?ｓ时，渗透系数 Ｋ４越大，渗透系数 Ｋ３对模型预测结果的正影响越大，
而当渗透系数 Ｋ３的值大于 ０．００２２５ｃｍ?ｓ时，渗透系数 Ｋ４越大，渗透系数 Ｋ３对模型预测结果的负影
响越大；当渗透系数 Ｋ４的值小于 ０．０００５ｃｍ?ｓ时，渗透系数 Ｋ３越大，渗透系数 Ｋ４对模型预测结果的
正影响越大，而当渗透系数 Ｋ４的值大于 ０．０００５ｃｍ?ｓ时，渗透系数 Ｋ３越大，渗透系数 Ｋ４对模型预测
结果的负影响越大。
５．２．３ 单个样本特征影响分析 从测试集中挑选两个预测样本，采用 ＳＨＡＰ理论解释输入特征对样本
预测结果的影响，如图 １０所示。图中横坐标为预测值的大小，纵坐标为输入特征的数值，红色表示
输入特征的 Ｓｈａｐｌｅｙ值为正，蓝色表示输入特征的 Ｓｈａｐｌｅｙ值为负；且红色和蓝色区域的面积越大，表

— １ ２ ４ —
０