Page 106 - 2024年第55卷第2期

态探测和共线性分析这四个方面详细研究了环境变量及其交互作用对降水空间分布的影响。随后构建
并探讨了基于像元的卷积神经网络降水降尺度模型，考察其在年、季、月和旬的性能表现以及模型参
数的变化情况。本研究填补了统计降水降尺度系列研究的最后一块拼图，建立了从降水降尺度环境变
量识别到高分辨率和高精度的降水产品生成的完整流程。
本文以消除降水场同质部分影响作为研究切入点，综合应用贝叶斯优化和高精度曲面建模算法，
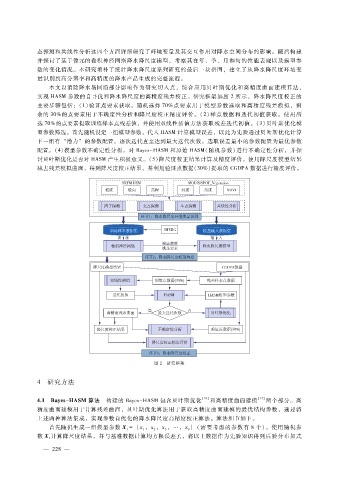
实现 ＨＡＳＭ参数的自寻优和降水降尺度的高精度残差校正。研究框架如图 ２所示，降水降尺度校正的
主要步骤包括：（ １）验证点要素获取。随机选择 ７０％点要素用于模型参数选取和高精度残差模拟，剩
余的 ３０％的点要素用于不确定性分析和降尺度校正精度评价。（２）样点数据和迭代初值获取。使用所
选 ７０％的点要素提取训练样本点残差值，并使用双线性插值方法获取残差迭代初值。（３）贝叶斯优化模
型参数筛选。首先随机设定一组模型参数，代入 ＨＡＳＭ计算模型误差，以此为先验通过贝叶斯优化计算
下一组有 “潜力” 的参数配置。逐次迭代直至达到最大迭代次数，选取误差最小的参数配置为最优参数
配置。（ ４）模型参数不确定性分析。对 Ｂａｙｅｓ － ＨＡＳＭ和原始 ＨＡＳＭ（随机参数）进行不确定性分析，并探
讨贝叶斯优化是否对 ＨＡＳＭ产生积极意义。（５）降尺度校正结果计算及精度评价。使用降尺度模型结果
减去残差模拟曲面，得到降尺度校正结果，并利用验证点数据（ ３０％）提取的 ＣＧＤＰＡ数据进行精度评价。

图 ２ 研究框架

４ 研究方法

４．１ Ｂａｙｅｓ － ＨＡＳＭ 算法 构建的 Ｂａｙｅｓ － ＨＡＳＭ包含贝叶斯优化 ［２４］ 和高精度曲面建模 ［１２］ 两个部分。高
精度曲面建模用于计算残差曲面，贝叶斯优化算法用于获取高精度曲面建模的最优结构参数，通过将
上述两种算法集成，实现参数自优化的降水降尺度高精度校正算法。算法细节如下。
首先随机生成一组模型参数 Ｘ ＝ ｛ｘ，ｘ，ｘ，…，ｘ｝ （需要考虑的参数有 ８个）。使用随机参
１ １ ２ ３ ８
数 Ｘ计算降尺度结果，并与基准数据计算均方根误差 ｆ，将以上数据作为先验知识得到后验分布如式
１
１
— ２ ２ —
８