Page 107 - 2024年第55卷第2期

（１）所示：
ｐ（ｆ ｜Ｘ，Ｆ，ｘ ） ＝Ｎ（ｍ，Σ ） （１）
 
式中：Ｘ ＝ ｛Ｘ，Ｘ，Ｘ，…，Ｘ｝为观测数据集的模型参数组合向量；Ｆ ＝ ｛ｆ，ｆ，ｆ，…，ｆ｝为观测
１ ２ ３ ｎ １ ２ ３ ｎ
数据集降水均方根误差；ｎ为迭代次数；ｘ 为一组预测模型参数组合；ｆ为代理模型的输出结果；ｍ
 
为后验分布的均值函数，Σ为后验分布的协方差矩阵。
使用由均值函数 ｍ和协方差矩阵 Σ构造的采集函数（式（２））会选择具有最大可能性提高当前最大
值的点作为下一个查询点。
＋
ｍ－ ｆ（ｘ） － ε
( ｔ )
Ｘ ＝ ａｒｇｍａｘ Φ （２）
ｔ ＋ １
Σ ｔ
为第 ｔ次
ｔ
式中：Φ（·）为正态分布累积分布函数；ｍ 为第 ｔ次迭代高斯过程概率密度函数的均值；Σ ｔ
＋
迭代高斯过程概率密度函数的方差；ｆ（ｘ）为前 ｔ次迭代的已知最大值；ａｒｇｍａｘ获取使 Φ（·）获得最
大值的参数；ε 为极小正数用来权衡探索和开发；Ｘ 为确定的下一次模型参数组合。
ｔ ＋ １
４．２ 精度评价指标 从两个角度对降尺度校正算法的表现进行评估，其一是采用蒙特卡洛算法 ［２５］ 对
模型的不确定性定量评估，用于衡量贝叶斯优化前后高精度曲面建模的不确定性；其二是采用 ４个定
量评价指标对降尺度校正结果精度评价，用于衡量使用算法校正前后精度的变化，这 ４个指标包括：
相关系数 ＣＣ（ｃｏｒｒｅｌａｔｉｏｎｃｏｅｆｆｉｃｉｅｎｔ）、相似指数 ＩＡ（ｉｎｄｅｘｏｆａｇｒｅｅｍｅｎｔ）、均方根误差 ＲＭＳＥ（ｒｏｏｔｍｅａｎ
ｓｑｕａｒｅｅｒｒｏｒ ）和相对偏差 ＲＢ（ｒｅｌａｔｉｖｅｂｉａｓ）。
降尺度校正过程需要实测降水数据用于模型训练和精度验证，然而滦河流域气象站点稀少，仅有
５个国家级气象站点，实测站点数据无法满足需求，故本研究选用了国家气象数据中心发布的 ２０１８年
ＣＧＤＰＡ（ＣｈｉｎａＧａｕｇｅ － ＢａｓｅｄＤａｉｌｙＰｒｅｃｉｐｉｔａｔｉｏｎＡｎａｌｙｓｉｓ）降水产品作为降水基准数据。此产品以中国大
陆国家级的雨量站点为基础生成 ［２６］ ，经过了严格的质量控制，多项研究将其用作降水基准数据 ［２７］ ，
精度值得信赖。最终，本研究使用的降水数据点共 ７５个，用于模型训练和验证的数据点分别为 ５２个
（约占总数的 ７０％）和 ２３个 （约占 总 数 的 ３０％），超 过 了 其 他 同 等 面 积 流 域 降 水 降 尺 度 研 究 样 本 数
量 ［２８］ ，足以支撑研究成果的准确性和可信度。

５ 结果分析

５．１ 模型不确定性评估 提供给蒙特卡洛算法的样本越多，统计结果越精确，但是 Ｂａｙｅｓ － ＨＡＳＭ算法
本身消耗算力较大，样本的增多会增加计算负担，因此需要合理分配算力和确定样本量以保障计算速
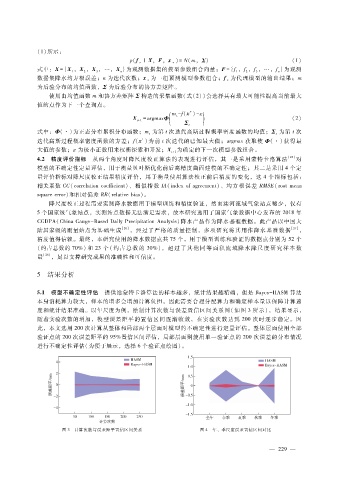
度和统计结果准确。以年尺度为例，绘制计算次数与误差置信区间关系图（如图 ３所示），结果显示，
随着实验次数的增加，模型误差距平的置信区间逐渐收敛，在实验次数达到 ２００次时逐步稳定。因
此，本文选用 ２００次计算从整体和局部两个层面对模型的不确定性进行定量评估。整体层面使用全部
验证点的 ２００次误差距平的 ９５％置信区间评估，局部层面则使用单一验证点的 ２００次误差的分布情况
进行不确定性评估（为便于展示，选择 ６个验证点绘图）。

图 ３ 计算次数与误差距平置信区间关系 图 ４ 年、季尺度误差置信区间对比

— ２ ２ ９ —