Page 108 - 2024年第55卷第2期

图 ４将年、季尺度原始 ＨＡＳＭ和 Ｂａｙｅｓ － ＨＡＳＭ的置信区间进行了对比。在年、季尺度下，相对于
原始 ＨＡＳＭ，Ｂａｙｅｓ － ＨＡＳＭ能够显著降低模型的不确定性，并将误差距平的置信区间稳定在 ０值附近，
而原始 ＨＡＳＭ的置信区间则有较大幅度的波动，其中不确定性下降最明显的是春季和冬季，误差距平
的置信区间从±０．８ｍｍ优化到±０．１ｍｍ，夏季、秋季和年尺度的不确定性也有不同程度的下降。出现
这种现象的主要原因是春冬季降水较少，模型参数的波动更容易影响残差的计算结果。
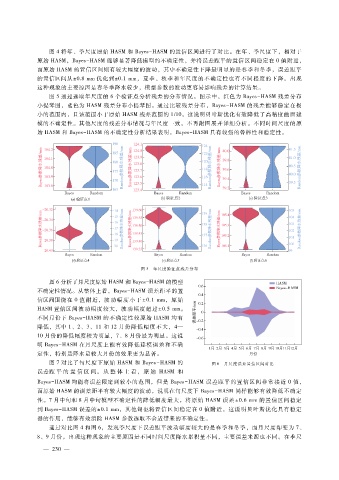
图 ５通过选取年尺度的 ６个验证点分析残差的分布情况。图示中，红色为 Ｂａｙｅｓ － ＨＡＳＭ残差分布
小提琴图，蓝色为 ＨＡＳＭ残差分布小提琴图。通过比较残差分布，Ｂａｙｅｓ － ＨＡＳＭ的残差能够稳定在极
小的范围内，且该范围小于原始 ＨＡＳＭ残差范围的 １?１０，这说明贝叶斯优化有效降低了高精度曲面建
模的不确定性。其他尺度的残差分布情况与年尺度一致，不再附图展开详细分析。不同时间尺度的原
始 ＨＡＳＭ和 Ｂａｙｅｓ － ＨＡＳＭ的不确定性分析结果表明，Ｂａｙｅｓ － ＨＡＳＭ具有较强的鲁棒性和稳定性。

图 ５ 年尺度验证点残差分布

图 ６分析了月尺度原始 ＨＡＳＭ和 Ｂａｙｅｓ － ＨＡＳＭ的模型
不确定性情况。从整体上看，Ｂａｙｅｓ － ＨＡＳＭ误差距平的置
信区间围绕在 ０值附 近，波 动幅 度小 于 ±０．１ｍｍ，原 始
ＨＡＳＭ置信区间波动幅度较大，波动幅度超过 ±０．５ｍｍ。
不同月份下 Ｂａｙｅｓ － ＨＡＳＭ 的不确定性较原始 ＨＡＳＭ 均有
降低，其中 １、２、３、１１和 １２月份降低幅度不大，４—
１０月份的降低幅度较为明显，７、８月份最为明显。这说
明 Ｂａｙｅｓ － ＨＡＳＭ在月尺度上能有效降低建模误差和不确
定性，特别是降水量较大月份的效果更为显著。
图 ７对比了旬尺度下原始 ＨＡＳＭ 和 Ｂａｙｅｓ － ＨＡＳＭ 的 图 ６ 月尺度误差置信区间对比
误差距 平 的 置 信 区 间。 从 整 体 上 看， 原 始 ＨＡＳＭ 和
Ｂａｙｅｓ － ＨＡＳＭ均能将误差限定到较小的范围，但是 Ｂａｙｅｓ － ＨＡＳＭ 误差距平的置信区间非常接近 ０值，
而原始 ＨＡＳＭ的误差距平有较大幅度的波动，说明在旬尺度下 Ｂａｙｅｓ － ＨＡＳＭ同样能够有效降低不确定
性。７月中旬和 ８月中旬模型不确定性的降低幅度最大，将原始 ＨＡＳＭ误差±０．６ｍｍ的置信区间稳定
到 Ｂａｙｅｓ － ＨＡＳＭ误差的±０．１ｍｍ，其他旬也将置信区间稳定在 ０值附近，这说明贝叶斯优化具有稳定
器的作用，能够有效消除 ＨＡＳＭ参数选取不合适带来的不确定性。
通过对比图 ４和图 ６，发现季尺度下误差距平波动幅度较大的是春季和冬季，而月尺度却变为 ７、
８、９月份。出现这种现象的主要原因是不同时间尺度降水累积量不同，主要误差来源也不同。在季尺

０
— ２ ３ —