Page 22 - 2021年第52卷第10期

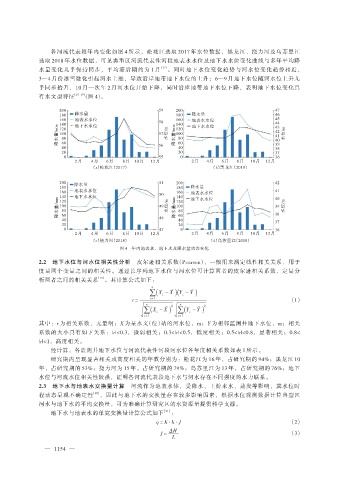
各河流代表段年内变化如图 4 所示，松花江选取 2017 年水位数据，黑龙江、挠力河及乌苏里江
选取 2018 年水位数据，可见典型区河流代表性河段地表水水位及地下水水位变化曲线与多年平均降
水量变化几乎保持同步，平均滞后期约为 1 月 ［17］ 。同时地下水位变化趋势与河水位变化趋势相近，
3—4 月份冰雪融化引起河水上涨，导致沿岸地带地下水位的上升；6—9 月地下水位随河水位上升几
乎同步抬升，10 月—次年 2 月河水位开始下降，同时沿岸地带地下水位下降，表明地下水位变化具
（图 4）。
有水文型特征 ［18-19］

200 59 200 47
180 降水量 180 降水量 46
160 地表水水位 160 地表水水位 45
58 140 地下水水位 44
140
地下水水位
降水量/mm 120 57 水位/m 降水量/mm 120 42 水位/m
43
100
100
41
80
80
40
60
40 56 60 39
40
38
20 20 37
0 55 0 36
2 月 4 月 6 月 8 月 10 月 12 月 2 月 4 月 6 月 8 月 10 月 12 月
（a）松花江（2017） （b）黑龙江（2018）
200 降水量 51 200 42
180 180 降水量
160 地表水水位 50 160 地表水水位 41
地下水水位
140
140
降水量/mm 120 49 水位/m 降水量/mm 120 39 水位/m
地下水水位
40
100
100
80
80
60
40
40 48 60 38
37
20 20
0 47 0 36
2 月 4 月 6 月 8 月 10 月 12 月 2 月 4 月 6 月 8 月 10 月 12 月
（c）挠力河（2018） （d）乌苏里江（2018）
图 4 年内地表水、地下水及降水量动态变化
2.2 地下水位与河水位相关性分析 皮尔逊相关系数（Pearson），一般用来测定线性相关关系，用于
度量两个变量之间的相关性。通过长序列地下水位与河水位可计算两者的皮尔逊相关系数，定量分
析两者之间的相关关系 ［19］ 。其计算公式如下：
n
å( X - X ˉ )(Y - Y ˉ )
i
i
r = i = 1 （1）
n n
2
å( X - X ˉ ) å(Y - Y ˉ ) 2
i
i
i = 1 i = 1
其中：r 为相关系数，无量纲；X 为某水文（位）站的河水位，m；Y 为相邻监测井地下水位，m；相关
系数的大小具有如下关系：|r|<0.3，微弱相关；0.3<|r|<0.5，低度相关；0.5<|r|<0.8，显著相关；0.8<
|r|<1，高度相关。
经计算，各监测井地下水位与河流代表性河段河水位各年度相关系数如表 1 所示。
研究期内呈现显著相关或高度相关的年数分别为：松花江为 16 年，占研究期的 94%；黑龙江 10
年，占研究期的 53%；挠力河为 15 年，占研究期的 79%；乌苏里江为 13 年，占研究期的 76%；地下
水位与河流水位相关性较强，证明各河流代表段地下水与河水存在不同强度的水力联系。
2.3 地下水与地表水交换量计算 河流作为地表水体，受降水、上游来水、蒸发等影响，其水位时
程动态呈现不确定性 ［20］ ，因此与地下水的交换量存在较多影响因素，根据水位观测数据计算典型区
河水与地下水的平均交换量，可为准确计算研究区的水资源量提供科学支撑。
地下水与地表水的单宽交换量计算公式如下 ［21］ ：
q = K ⋅ h ⋅ J （2）
J = ΔH （3）
L

— 1154 —