Page 47 - 2021年第52卷第10期

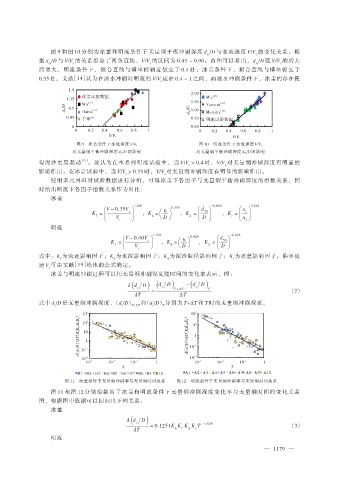
图 9 和图 10 分别为冰盖和明流条件下无量纲平衡冲刷深度 d /D 与水流强度 V/V 的变化关系。根
c
se
据 d /D 与 V/V 的关系拟合了两条直线，V/V 的区间为 0.45 ~ 0.90。由图可以看出，d /D 随 V/V 的增大
c
c
se
se
c
而增大，明流条件下，拟合直线与横坐标轴近似交于 0.4 处；冰盖条件下，拟合直线与横坐标交于
0.35 处。文献 ［14］ 认为在清水冲刷时明流的 V/V 应在 0.4 ~ 1 之间，而清水冲刷条件下，冰盖的存在使
c
1.8
2.00
冰盖试验数据 Mia ［17］
1.35
［13］ 1.50 Yanmaz ［18］
Wu
d se/D 0.9 Hains ［11］ d se/D 1.00 Melville ［14］
0.45 王军 ［9］ 0.50 明流试验数据
0 0.00
0 0.2 0.4 0.6 0.8 1 0 0.2 0.4 0.6 0.8 1
V/V c
V/V c
图 9 冰盖条件下水流强度 V/V c 图 10 明流条件下水流强度 V/V c
对无量纲平衡冲刷深度 d se/D 的影响 对无量纲平衡冲刷深度 d se/D 的影响
得泥沙更易起动 ［12］ 。故认为在本系列明流试验中，当 V/V ＞0.4 时，V/V 对无量纲冲刷深度有明显的
c
c
影响作用；在冰盖试验中，当 V/V ＞0.35 时，V/V 对无量纲冲刷深度有明显的影响作用。
c
c
使用多元回归对试验数据进行分析，可得冰盖下各因子与无量纲平衡冲刷深度的指数关系，同
时给出明流下各因子指数关系作为对比：
冰盖
æV - 0.35V ö 1.240 æ h ö 0.350 æ d ö -0.060 æ n ö 0.244
K = ç ç c ÷ ÷ ，K = ç ÷ ，K = ç ç 50 ÷ ÷ ，K = ç ç i ÷ ÷
I
d
r
h
è V c ø è D ø è D ø è n b ø
明流
æ V - 0.40V ö 1.150 æ h ö 0.426 æ d ö -0.425
K = ç c ÷ ，K = ，K = ç 50 ÷
h
I
d
è V c ø è D ø è D ø
式中：K 为流速影响因子；K 为水深影响因子；K 为泥沙粒径影响因子；K 为冰盖影响因子；临界流
r
d
I
h
速 V 可由文献 ［19］ 给出的公式确定。
c
冰盖与明流冲刷过程可以用无量纲冲刷深度随时间的变化率表示，即：
d ( d s D ) ( d s D ) T + ΔT - ( d s D ) T
dT = ΔT （2）
式中 d /D 是无量纲冲刷深度，（d /D） T+ΔT 和（d /D） 分别为 T+ΔT 和 T 时的无量纲冲刷深度。
s
s
T
s
3 2
10
（K IK yDK dK r ） 10 2 （K IK yDK d） 10 1
10
10
（d s/D）dT / 10 -1 1 （d s/D）dT / 10 -1
d
10 -2 d 10 -2
10 -3 10 -2 10 -1 1 10 -3 10 -2 10 -1 1
T T
B1 B2 B3 B4 B5 B6 B7 B8 B9 B10 A1 A2 A3 A4 A5 A6 A7 A8 A9 A10
图 11 冰盖条件下无量纲冲刷率与无量纲时间关系 图 12 明流条件下无量纲冲刷率与无量纲时间关系
图 11 和图 12 分别绘制出了冰盖和明流条件下无量纲冲刷深度变化率与无量纲时间的变化关系
图，根据图中数据可以回归出下列关系：
冰盖
d ( d s D ) -1.026
dT = 0.1251K K K K T （3）
h
I
r
d
明流
— 1179 —