Page 48 - 2021年第52卷第10期

d ( d s D )
dT = 0.0391K K K T -1.068 （4）
h
d
I
对（3）式进行积分可得出冰盖下 d /D 与无量纲时间 T 的经验关系，对比可得出对应明流条件：
s
冰盖
d s æV - 0.35V c ö 1.240 æ h ö 0.350 æ d 50 ö -0.060 æ n i ö 0.244 -0.026 )
D = ç ç è V c ÷ ÷ ø ç è D ÷ ø ç ç è D ÷ ÷ ø ç ç è n b ÷ ÷ ( 5.77 - 3.91T （5）
ø
明流
d s æV - 0.40V c ö 1.150 æ h ö 0.426 æ d 50 ö -0.425 -0.068 )
D = ç ç è V c ÷ ÷ ø ç è D ÷ ø ç ç è D ÷ ÷ ø ( 1.19 - 0.67T （6）

［14］
式中平衡冲刷深度 t 采用 Melville 中给出的计算形式，冰盖条件下加入冰盖糙率因子 n /n 进行回归
e
i
b
分析，代入本系列试验数据回归分析得平衡冲刷时间关系式如下：
冰盖
æ
6 D V öæ n i ö 1.35
t = 1.5 × 10 ç ç - 0.35 ÷ ÷ç ç ÷ ÷ （7）
e V è V c øè n b ø
明流
æ
6 D V ö
t = 3.1 × 10 V ç ç è V c - 0.40 ÷ ÷ ø （8）
e
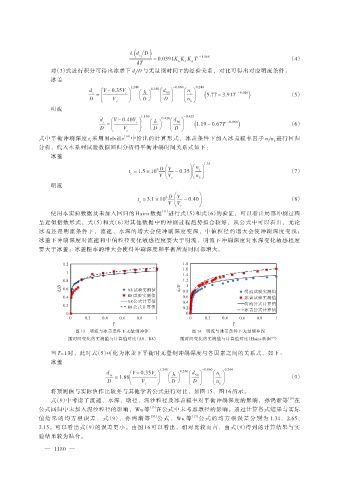
使用本实验数据及未加入回归的 Hains 数据 ［11］ 进行式（5）和式（6）的验证，可以看出局部冲刷过程
呈近似指数形式，式（5）和式（6）对其他数据中的冲刷过程趋势拟合较好，从公式中可以看出，无论
冰盖还是明流条件下，流速、水深的增大会使冲刷深度变深，中值粒径的增大会使冲刷深度变浅；
冰盖下冲刷深度对流速和中值粒径变化敏感程度要大于明流，明流下冲刷深度对水深变化敏感程度
要大于冰盖；冰盖糙率的增大会使得冲刷深度和平衡所需时间都增大。

1.2 1.8
1.6
1
1.4
0.8 1.2
d s/D 0.6 A8 试验实测值 d s/D 0.8 1 明流试验实测值
B8 试验实测值
0.4 0.6 冰盖试验实测值
A8 公式计算值 0.4
0.2 B8 公式计算值 明流公式计算值
0.2
冰盖公式计算值
0 0
0 0.2 0.4 0.6 0.8 1 0 0.2 0.4 0.6 0.8 1
T T
图 13 明流与冰盖条件下无量纲冲深 图 14 明流与冰盖条件下无量纲冲深
随时间变化的实测值与计算值对比（A8、B8） 随时间变化的实测值与计算值对比（Hains 数据 ）
[11]
当 T=1 时，此时式（5）可化为冰盖下平衡时无量纲冲刷深度与各因素之间的关系式，如下：
冰盖
d æV - 0.35V ö 1.240 0.350 æ d ö -0.060 æ n ö 0.244
se = 1.86 ç ç c ÷ ÷ æ h ö ÷ ç ç 50 ÷ ÷ ç ç i ÷ ÷ （9）
ç
D è V c ø è D ø è D ø è n b ø
将预测值与实际值作比较并与其他学者公式进行对比，如图 15、图 16 所示。
式（9）中考虑了流速、水深、墩径、泥沙粒径及冰盖糙率对平衡冲刷深度的影响，孙鸿渐等 ［20］ 在
公式回归中未加入泥沙粒径的影响，Wu 等 ［13］ 在公式中未考虑墩径的影响。通过计算各式结果与实际
值 结 果 的 均 方 根 误 差 ， 式（9）、 孙 鸿 渐 等 ［20］ 公 式 、 Wu 等 ［13］ 公 式 的 均 方 根 误 差 分 别 为 1.34、 2.65、
2.15。可以看出式（9）的误差更小。由图 16 可以看出，相对比较而言，由式（9）得到的计算结果与实
验结果较为贴合。

— 1180 —