Page 109 - 2022年第53卷第6期

的混凝土坝变形行为分析能力尚显匮乏。相反，ＨＴＴ模型常采用坝体混凝土与基岩温度测值计算热变
形，但该模型存在难以有效选取合理表征坝体混凝土温度场的温度测值的困难，且可能因引入较多的
温度因子导致模型结构复杂甚至引发维数灾难 ［３０］ 。

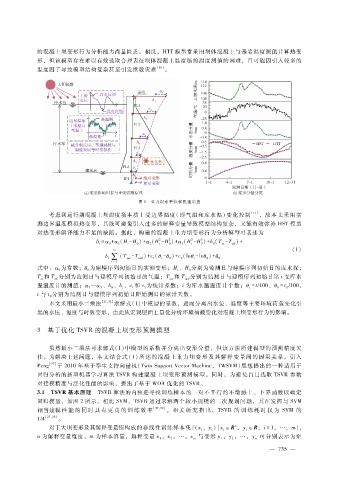
图 １ 重力坝水平位移机理示意

考虑到运行期混凝土坝温度场本质上受边界温度（即气温和库水温）变化控制 ［１１］ ，故本文采用实
测边界温度模拟热变形，其既可避免引入过多的解释变量导致模型结构复杂，又能有效弥补 ＨＳＴ模型
对热变形解译能力不足的缺陷。据此，构建的混凝土重力坝变形行为分析模型可表述为
２ ２ ３ ３
ｔ
δ ｔ α ０ α １ ｔ ０ （Ｈ － Ｈ） ＋ α ３ （Ｈ － Ｈ） ＋ ｂ（Ｔ － Ｔ ） ＋
＝ ＋ （Ｈ－ Ｈ） ＋ α ２
ａｔ
０
０
ａ０
０
ｔ
ｍ （１）
ｉ∑
ｂ （Ｔ － Ｔ ） ＋ ｃ（ θ ｔ θ ０ ２ － ｌｎ θ ０ ） ＋ δ ０
－ ） ＋ ｃ（ｌｎ θ ｔ
１
ｉｗｔ
ｉｗ０
ｉ ＝１
为建模序列初始日的实测变形；Ｈ、Ｈ分别为监测日与建模序列初始日的库水深；
式中：α ０ 为常数；δ ０ ｔ ０
Ｔ 和 Ｔ 分别为监测日与建模序列初始日的气温；Ｔ 和 Ｔ 分别为监测日与建模序列初始日第 ｉ支库水
ａｔ ａ０ ｉｗｔ ｉｗ０
＝ ｔ?１００，
０ ｉ １ ２ ０
温温度计的测值；α １ —α ３ 、ｂ、ｂ、ｃ和 ｃ为统计系数；ｉ为库水温温度计个数；θ ｔ ＝ ｔ?１００、θ ０
ｔ与 ｔ分别为监测日与建模序列初始日距始测日的累计天数。
０
本文采用最小二乘法 ［１１，３１］ 求解式（１）中模型的系数，进而分离出水位、温度等主要环境荷载变化引
起的水压、温度与时效变形，由此从宏观层面上量化分析环境荷载变化对混凝土坝变形行为的影响。
３ 基于优化 ＴＳＶＲ的混凝土坝变形预测模型
虽然最小二乘法可求解式（１）中模型的系数并分离出变形分量，但该方法所建模型的预测精度欠
佳。为解决上述问题，本文结合式 （１）所述的混凝土重力坝变形及其解释变量间的因果关系，引入
［２７］
Ｐｅｎｇ 于 ２０１０年基于孪生支持向量机（ＴｗｉｎＳｕｐｐｏｒｔＶｅｃｔｏｒＭａｃｈｉｎｅ，ＴＷＳＶＭ）思想提出的一种适用于
回归分析的新型机器学习算法 ＴＳＶＲ构建混凝土坝变形预测模型。同时，为避免盲目选取 ＴＳＶＲ参数
对建模精度与泛化性能的影响，提出了基于 ＷＯＡ优化的 ＴＳＶＲ。
３．１ ＴＳＶＲ基本原理 ＴＳＶＲ算法的内核是寻找训练样本的一对不平行的不敏感上、下界函数以确定
回归模型，如图 ２所示。相比 ＳＶＭ，ＴＳＶＲ通过求解两个较小规模的二次规划问题，其在发挥与 ＳＶＭ
相当建模 性 能 的 同 时 具 有 更 高 的 训 练 效 率 ［２７，３２］ 。 相 关 研 究 指 出，ＴＳＶＲ的 训 练 耗 时 仅 为 ＳＶＭ 的
１?４ ［２７，３３］ 。
ｎ
对于大坝变形及其解释变量所构成的非线性训练样本集｛（ｘ，ｙ） ｘ ∈Ｒ，ｙ ∈Ｒ，ｉ ＝ １ ，…，ｍ｝，
ｉ
ｉ
ｉ
ｉ
ｎ为解释变量维度，ｍ为样本容量，解释变量 ｘ，ｘ，…，ｘ 与变形 ｙ，ｙ，…，ｙ 可分别表示为矩
１ ２ ｍ １ ２ ｍ
— ７ ３ ５ —