Page 53 - 2023年第54卷第7期
P. 53
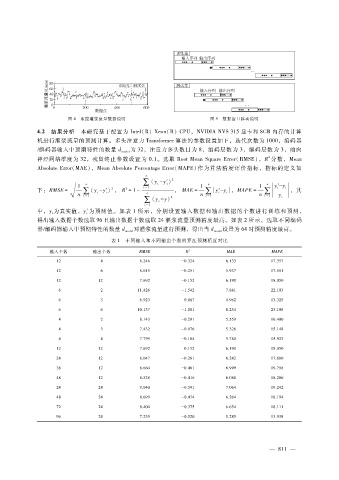
图 4 监控灌浆流量数据说明 图 5 数据窗口移动说明
4.2 结果分析 本研究基于配置为 Intel(R)Xeon(R)CPU,NVIDIANVS315显卡和 8GB内存的计算
机进行灌浆流量的预测计算。多头注意力 Transformer算法的参数设置如下,迭代次数为 1000,编码器
?解码器输入中预期特性的数量 d 为 32,注意力多头数目为 8,编码层数为 3,解码层数为 3,前向
model
2
神经网络维度为 32,残留终止参数设置为 0.1。选取 RootMeanSquareError(RMSE),R分数,Mean
AbsoluteError (MAE),MeanAbsolutePercentageError(MAPE)作为算法精度评价指标,指标的定义如
n
∑ (y- y′ ) 2
i
i
1 n i =1 1 n 1 n y′ - y
i
i
2
2
下:RMSE = ∑ (y- y′) , R = 1 - , MAE= ∑ y′ - y ,MAPE= ∑ ,其
槡 n 2 n i =1 n i =1 y
i
i
i
i
n i =1
i
∑ (y- 珋
y)
i
i =1
中,y为真实值,y′为预测值。如表 1所示,分别设置输入数据和输出数据的个数进行训练和预测,
i i
得出输入数据个数选取 96且输出数据个数选取 24灌浆流量预测精度最高。如表 2所示,选取不同编码
器?解码器输入中预期特性的数量 d 对灌浆流量进行预测,得出当 d 设置为 64时预测精度最高。
model model
表 1 不同输入和不同输出个数的算法预测精度对比
输入个数 输出个数 RMSE R 2 MAE MAPE
12 4 8.246 - 0.324 6.133 17.357
12 6 8.015 - 0.251 5.937 17.581
12 12 7.692 - 0.152 6.190 18.050
6 2 11.426 - 1.542 7.881 22.103
6 3 6.923 0.067 4.962 13.325
6 6 10.137 - 1.001 8.254 23.108
4 2 8.143 - 0.291 5.559 16.400
4 3 7.432 - 0.076 5.326 15.148
4 4 7.799 - 0.184 5.780 15.923
12 12 7.692 - 0.152 6.190 18.050
24 12 8.047 - 0.261 6.242 17.880
36 12 8.664 - 0.461 6.999 19.798
48 12 8.528 - 0.416 6.088 18.206
24 24 9.040 - 0.591 7.064 19.242
48 24 8.699 - 0.474 6.264 18.194
72 24 8.404 - 0.375 6.654 18.111
96 24 7.239 - 0.020 5.285 13.938
— 8 1 1 —