Page 35 - 2023年第54卷第12期
P. 35
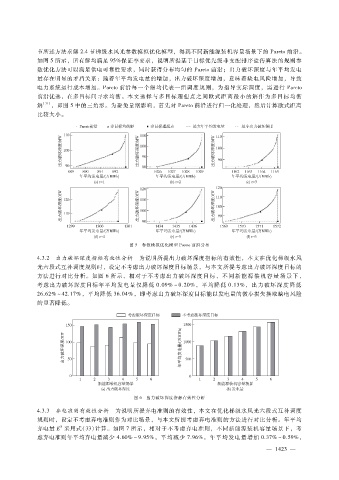
节所述方法求解 2.4节梯级水风光参数模拟优化模型,得到不同新能源装机容量场景下的 Pareto前沿。
如图 5所示,所有解均满足 95%保证率要求,说明所提基于目标优先级非支配排序遗传算法的规则参
数优化方法可以满足供电可靠性要求,同时获得分布均匀的 Pareto前沿;出力破坏深度与年平均发电
量存在明显的矛盾关系:随着年平均发电量的增加,出力破坏深度增加,意味着缺电风险增加,导致
电力系统运行成本增加。Pareto前沿每一个解均代表一组调度规则,为指导实际调度,需进行 Pareto
前沿优选,在多目标间寻求均衡。本文选择与多目标理想点之间欧式距离最小的解作为多目标均衡
解 [31] ,即图 5中的三角形。为避免量纲影响,首先对 Pareto前沿进行归一化处理,然后计算欧式距离
比较大小。
图 5 参数模拟优化模型 Pareto前沿分布
4.3.2 出力破坏深度指标有效性分析 为说明所提出力破坏深度指标的有效性,本文在优化梯级水风
光六段式互补调度规则时,设定不考虑出力破坏深度目标场景,与本文所提考虑出力破坏深度目标的
方法进行对比分析。如图 6所示,相对于不考虑出力破坏深度目 标,不 同 新 能 源 装 机 容 量 场 景 下,
考虑出力破坏深度目标年平均发电量仅降低 0.09%~0.20%,平均降低 0.13%,出力破坏深度降低
26.62%~42.17%,平均降低 36.04%,即考虑出力破坏深度目标能以发电量的微小损失换取缺电风险
的显著降低。
图 6 出力破坏深度指标有效性分析
4.3.3 弃电准则有效性分析 为说明所提弃电准则的有效性,本文在优化梯级水风光六段式互补调度
规则时,设定不考虑弃电准则作为对比场景,与本文所提考虑弃电准则的方法进行对比分析。年平均
S
弃电量 E 采用式(33)计算。如图 7所示,相对于不考虑弃电准则,不同新能源装机容量场景下,考
虑弃电准则年平均弃电量减少 4.60%~9.95%,平均减少 7.96%,年平均发电量增加 0.37%~0.59%,
4
— 1 2 3 —