Page 67 - 2023年第54卷第12期

图 ３ 不同方案叶片载荷分布图

表 １ 不同方案叶片载荷分布参数
前盖板流线 后盖板流线
方案
ＮＣ ＮＤ ＳＬＯＰＥ ＬＥ ＮＣ ＮＤ ＳＬＯＰＥ ＬＥ
方案一 ０．２１ ０．８１６ － ０．４５ ０ ０．１９ ０．８５３ ０．５ ０

方案二 ０．２５ ０．６８４ １ ０ ０．３８ ０．７１ ０．８５１ ０．０８

方案三 ０．１ ０．７８ ０．９５ ０ ０．１ ０．６５ １ ０
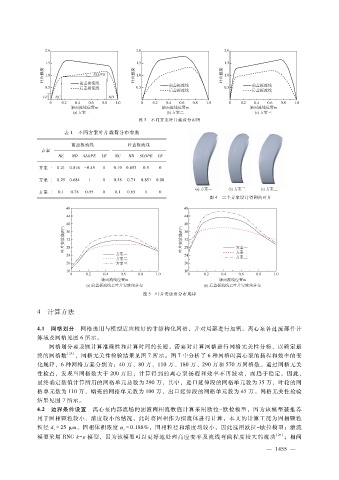
图 ４ 三个方案设计得到的叶片

图 ５ 叶片安放角分布规律

４ 计算方法

４．１ 网格划分 网格选用与模型适应较好的非结构化网格，并对局部进行加密。离心泵各过流部件计
算域及网格见图 ６所示。
网格划分要兼顾计算准确性和计算时间的长短，需要对计算网格进行网格无关性分析，以确定最
终的网格数 ［２５］ ，网格无关性检验结果见图 ７所示。图 ７中分析了 ６种网格时离心泵的扬程和效率的变
化规律，６种网格方案分别为：４０万、８０万、１１０万、１８０万、２９０万和 ５７０万网格数。通过网格无关
性检查，发现当网格数大于 ２００万后，计算得到的离心泵扬程和效率不再波动，而趋于稳定。因此，
最终确定数值计算所用的网格单元总数为 ２９０万，其中，进口延伸段的网格单元数为 ３５万，叶轮的网
格单元数为 １１０万，蜗壳的网格单元数为 １００万，出口延伸段的网格单元数为 ４５万。网格无关性检验
结果见图 ７所示。
４．２ 边界条件设置 离心泵内部流场的固液两相流数值计算采用欧拉－ 欧拉模型，因为该模型被推荐
用于固相颗粒较小、浓度较小的情况，此时将固相作为拟流体进行计算，本文的计算工况为固相颗粒
＝ ０．１８８％，固相粒径和浓度均较小，因此选用欧拉－ 欧拉模型；湍流
粒径 ｄ＝ ２５μ ｍ，固相体积浓度 α ｓ
ｓ
模型采用 ＲＮＧｋ － ε 模型，因为该模型可以更好地处理高应变率及流线弯曲程度较大的流动 ［２６］ ；相间
４
— １ ５ ５ —