Page 55 - 2025年第56卷第5期

组是否异常的做法过于绝对。为此本文采用健康与正常状态的数据差异进行检测的思路，把区间预测
引入水电机组的振动异常检测领域，将数据不稳定性以及模型局限性考虑在内。结合滑动窗口与区间
覆盖率，提出动态区间覆盖率，即计算滑动窗口内的区间覆盖率，进行振动趋势异常检测。
为验证区间预测是否能够展现出正常与异常状态的区别，以置信水平 Ｐ设为 ９０％，滑动窗口宽度 Ｗ
设为 １５，滑动步长 Ｓ设为 ５为例，引用 “ＭａＤａｔａ”和 “ＫｅｏｇｈＤａｔａ” 两个异常模拟数据集 ［１９］ 进行验证。
ＭａＤａｔａ数据集由下式生成的两个时间序列组成 ［１９］ ：
４０ π
Ｘ（ｔ） ＝ｓｉｎ ( )
ｔ＋ ｎ（ｔ）
１ Ｎ
（ ４）
４０ π
Ｘ（ｔ） ＝ｓｉｎ ( )
ｔ＋ ｎ（ｔ） ＋ ｅ（ｔ）
２ Ｎ Ｘ
式中：ｔ ＝ １，２，…，Ｎ，Ｎ ＝ １２００；ｎ（ｔ）是均值为 ０，标准差为 ０．１的加性高斯噪声。
ｅ（ｔ），ｔ ∈［６００，６２０］
１
ｅ（ｔ），ｔ ∈［８３０，８５０］
２
ｅ（ｔ） ＝ （５）
Ｘ
ｅ（ｔ），ｔ ∈［１０００，１１００］
３
０，其他
式中 ｅ （ｔ）遵循 Ｎ（０，０．５）的正态分布。由式（４）（５）可知，时间序列 Ｘ（ｔ）是有 １２００个点的正常时
１，２，３ １
间序列，添加异常事件后得到 Ｘ（ｔ），分别选取区间［６００，６２０］、［８３０，８８０］、［１０００，１１００］作为异
２
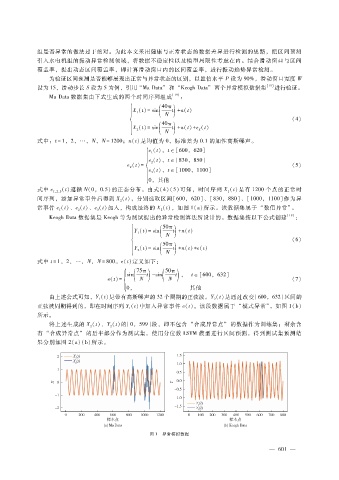
常事件 ｅ（ｔ）、ｅ（ｔ）、ｅ（ｔ）加入，构成最终的 Ｘ（ｔ），如图 １（ａ）所示。该数据集属于 “数值异常”。
１ ２ ３ ２
ＫｅｏｇｈＤａｔａ数据集是 Ｋｅｏｇｈ等为测试提出的异常检测算法所设计的。数据集按以下公式创建 ［１９］ ：
( )
Ｙ（ｔ） ＝ｓｉｎ ５０ π ｔ＋ ｎ（ｔ）
１
Ｎ
（６）
( )
Ｙ（ｔ） ＝ｓｉｎ ５０ π ｔ＋ ｎ（ｔ） ＋ ｅ（ｔ）
２
Ｎ
式中 ｔ ＝ １ ，２，…，Ｎ，Ｎ ＝ ８００ 。ｅ（ｔ）定义如下：
( ) ( )
{ ｓｉｎ ７５ π ｔ－ ｓｉｎ ５０ π ｔ， ｔ ∈［６００，６３２］
ｅ（ｔ） ＝ Ｎ Ｎ （７）
０， 其他
由上述公式可知，Ｙ（ｔ）是带有高斯噪声的 ３２个周期的正弦波。Ｙ（ｔ）是通过改变［６００，６３２］区间的
２
１
正弦波周期得到的，即在时间序列 Ｙ（ｔ）中加入异常事件 ｅ（ｔ）。该段数据属于 “模式异常”，如图 １（ｂ）
１
所示。
将上述生成的 Ｘ（ｔ）、Ｙ（ｔ）的［０，５９９］段，即不包含 “合成异常点” 的数据作为训练集；剩余含
２ ２
有 “合成异常点” 的后半部分作为测试集。使用分位数 ＬＳＴＭ模型进行区间预测，得到测试集预测结
果分别如图 ２（ａ）（ｂ）所示。

图 １ 异常模拟数据

— ６ ０ １ —