Page 67 - 水利学报2021年第52卷第6期

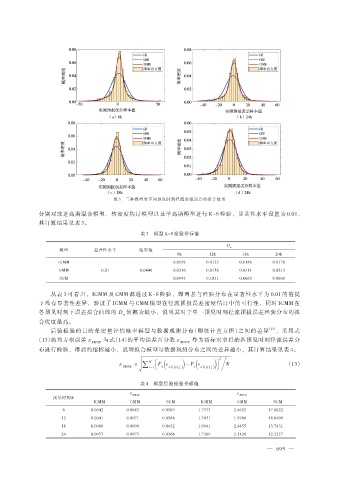
图 3 三种模型对不同预见时刻径流预报误差的拟合效果
分别对改进高斯混合模型、核密度估计模型以及单高斯模型进行 K-S 检验，显著性水平设置为 0.01，
其计算结果见表 3。

表 3 模型 K-S 检验指标值
D n
模型 显著性水平 临界值
6h 12h 18h 24h
IGMM 0.0158 0.0123 0.0186 0.0178
GMM 0.01 0.0440 0.0216 0.0156 0.0311 0.0213
SGM 0.0947 0.1031 0.0663 0.0660

从表 3 可看出，IGMM 及 GMM 都通过 K-S 检验，即两者与经验分布在显著性水平为 0.01 的前提
下没有显著性差异，验证了 IGMM 与 GMM 模型在径流预报误差密度估计中的可行性，同时 IGMM 在
各预见时刻下误差拟合曲线的 D 值都为最小，说明其对于单一预见时刻径流预报误差经验分布的拟
n
合优度最高。
后验检验的目的是定量评估概率模型与数据观测分布（即统计直方图）之间的差异 ［25］ ，采用式
（13）的均方根误差 ε RMSE 与式（14）的平均误差百分数 ε MAPE 作为指标对求得的各预见时刻径流误差分
布进行检验，得到的指标越小，说明拟合模型与数据观测分布之间的差异越小，其计算结果见表 4。
N æ
ε RMSE = å i = 1 çF e ) - F e ) ö ÷ ø 2 N （13）
t( x ( ) i t ( ) j
n( x ( ) i t ( ) j
è
表 4 模型后验检验指标值
ε RMSE ε MAPE
预见时刻/h
IGMM GMM SGM IGMM GMM SGM
6 0.0042 0.0083 0.0589 1.7573 2.4622 17.8822
12 0.0041 0.0071 0.0586 1.3031 1.9966 18.8490
18 0.0060 0.0096 0.0432 1.6941 2.4455 13.7431
24 0.0057 0.0075 0.0366 1.7389 2.1126 12.2327

— 695 —