Page 68 - 水利学报2021年第52卷第6期

| ) ) |
| | F e - F e | |
n( x ( ) i t ( ) j
t( x ( ) i t ( ) j
N
ε MAPE = 1 å i = 1 | | × 100% | | （14）
n
| | | F e ) | | |
n( x ( ) i t ( ) j
由表 4 可见，对于所有预见时刻而言，基于 IGMM 得到的误差分布的 ε RMSE 都保持在 0.06 及以
下 ， ε MAPE 都 保 持 在 1.8 以 下 ， 相 较 于 SGM 与
GMM，在两指标上的表现最好，说明基于 IGMM
得到的各预见时刻误差分布与数据观测分布之
间的差异相差最小。
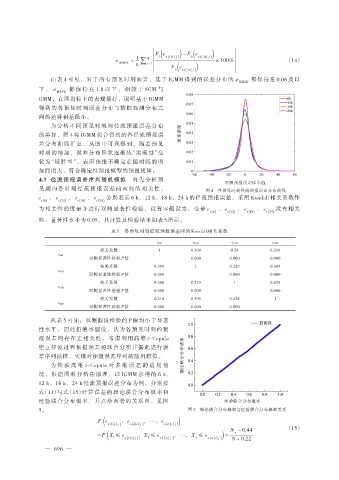
为分析不同预见时刻间径流预报误差分布
的差异，图 4 将 IGMM 拟合得到的各径流预报误 概率密度
差分布曲线汇总，从图中可观察到，随着预见
时刻的增加，误差分布形状逐渐从“尖瘦型”变
化为“矮胖型”，表面预报不确定在随时间的增
加而增大，符合确定性预报模型的预报规律。
4.3 径流预报误差序列随机模拟 首先分析预
实测预报误差样本值
见 期 内 各 时 刻 径 流 预 报 误 差 两 两 间 的 相 关 性 ，
图 4 各预见时刻径流预报误差分布曲线
e 、 e 、 e 、 e 分别表示 6 h、12 h、18 h、24 h 的径流预报误差，采用 Kendall 相关系数作
12
18
24
t ( ) 6 t ( ) t ( ) t ( )
为相关性的度量并进行双侧显著性检验，设置零假设为：变量 e 、 e 、 e 、 e 没有相关
t ( ) 6 t ( ) t ( ) t ( )
24
12
18
性，显著性水平为 0.05，其计算及检验结果如表 5 所示。
表 5 各预见时刻径流预报误差间的 Kendall 相关系数
e t(6) e t(12) e t(18) e t(24)
相关系数 1 0.309 0.28 0.218
e t(6)
双侧显著性检验 P 值 0.000 0.000 0.000
相关系数 0.309 1 0.329 0.305
e t(12)
双侧显著性检验 P 值 0.000 0.000 0.000
相关系数 0.280 0.329 1 0.428
e t(18)
双侧显著性检验 P 值 0.000 0.000 0.000
相关系数 0.218 0.305 0.428 1
e t(24)
双侧显著性检验 P 值 0.000 0.000 0.000

从表 5 可知，双侧假设检验的 P 值均小于显著
性水平，因此拒绝零假设，认为各预见时刻的预
报 误 差 均 存 在 正 相 关 性 ， 考 虑 利 用 高 维 t-Copula
建立径流过程预报误差的联合分布并据此进行误
差序列抽样，实现对预报误差序列的随机模拟。 理论联合分布概率
为 检 验 高 维 t-Copula 对 多 维 误 差 的 适 用 情
况，根据图形分析法原理，以 IGMM 求得的 6 h、
12 h、18 h、24 h 径流预报误差分布为例，分别按
式（11）与式（15）计算误差的理论联合分布概率和
经验联合分布概率，并点绘两者的关系图，见图 经验联合分布概率
5。 图 5 理论联合分布概率与经验联合分布概率关系

F e ，e ，，e
( x ( ) 1 t ( ) j x ( ) 2 t ( ) j x ( ) n t ( ) ) j （15）
(
q
= P X ≤ e x ( ) 1 t ( ) j ，X ≤ e x ( ) 2 t ( ) j ，，X ≤ e x ( ) n t ( ) ) j = N - 0.44
n
2
1
N + 0.22
— 696 —