Page 77 - 2021年第52卷第7期

图 3 数值模拟与试验外特性对比

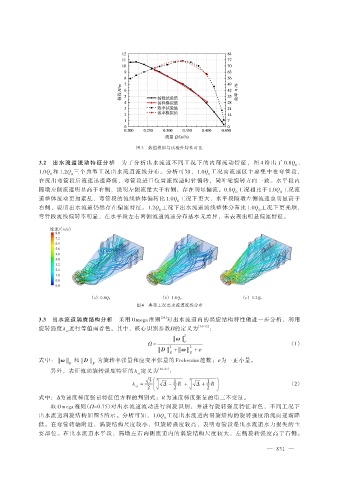
3.2 出水流道流动特征分析 为了分析出水流道不同工况下的内部流动特征，图 4 给出了 0.8Q 、
0
1.0Q 和 1.2Q 三个典型工况出水流道流线分布。分析可知，1.0Q 工况高流速区主要集中在弯管段，
0 0 0
在流出弯管段后流速迅速降低，弯管段进口位置流线逆时针偏转，同叶轮旋转方向一致。水平段内
隔墩左侧流速明显高于右侧，说明左侧流量大于右侧，存在明显偏流。0.8Q 工况相比于 1.0Q 工况流
0 0
道整体流动更加紊乱，弯管段的流线整体偏转比 1.0Q 工况下更大，水平段隔墩左侧流速也明显高于
0
右侧，说明出水流道仍然存在偏流特征。1.2Q 工况下出水流道流线整体分布比 1.0Q 工况下更光顺，
0 0
弯管段流线偏转不明显，在水平段左右两侧流道流速分布基本无差异，未表现出明显偏流特征。

流速/（m/s）

（a） 0.8Q 0 （b） 1.0Q 0 （c） 1.2Q 0
图 4 典型工况出水流道流线分布
3.3 出水流道涡旋结构分析 采用 Omega 准则 ［24］ 对出水流道内的涡旋结构特性做进一步分析，利用
旋转强度λ 进行等值面着色。其中，核心识别参数Ω的定义为 ［24-25］ ：
ci
  2
ω
Ω = F （1）
D
  +   + ε
2
2
ω
F F
D
ω
式中：   和   为旋转率张量和应变率张量的 Frobenius 范数；ε为一正小量。
F F
另外，表征流动旋转强度特征的λ 定义为 ［26-27］ ：
ci
3 æ 3 3 ö
λ = ç Δ - 1 R + Δ + 1 R ÷ （2）
ci
2 è 2 2 ø
式中：Δ为速度梯度张量特征值方程的判别式；R 为速度梯度张量的第三不变量。
取 Omega 准则（Ω=0.75）对出水流道流动进行涡旋识别，并进行旋转强度特征着色，不同工况下
出水流道涡旋结构如图 5 所示。分析可知，1.0Q 工况出水流道内涡旋结构的旋转强度沿流向逐渐降
0
低。在弯管转轴附近，涡旋结构尺度较小，但旋转强度较高，表明弯管段是出水流道水力损失的主
要部位。在出水流道水平段，隔墩左右两侧流道内的涡旋结构尺度较大，左侧旋转强度高于右侧。
— 831 —