Page 100 - 2022年第53卷第5期

式中：Q 为闸门自由出流过闸流量，m /s；μ 为过
3
0
闸流量系数，仅与闸前水深和闸门开度有关；E 为 0.008
下游闸门开度，m；B为闸门宽度，m；H 为下游闸 0.007
0
前水深，m；g为重力加速度，取9.81 m/s 。 0.006
2
渠池 A 长 7000 m，假设只有一个分水口，可能 0.005
位于x=0、x=0.5L 、x=L 、x=0.5（L+L ）或x=L等五处 0.004
u
u
u
（如图 2 所示，x 为分水口距上游闸门的距离，x=0 总体标准差/m 0.003
表示分水口位于上游闸后断面，x=L 表示分水口位
0.002
于下游闸前断面）。T=1 h 时分水口发生阶跃取水工
况，取水流量为 1 m /s，观察 ID 模型预测结果与非 0.001
3
恒定流仿真结果的差异。本文非恒定流仿真在“输 0.000
/
0 L u /2 L u （L u +L）2 L x
水渠道系统运行仿真与控制”软件 ［21］ 上进行，该软 分水口位置
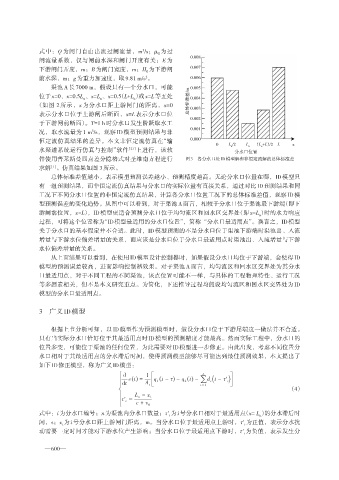
件使用普莱斯曼四点差分隐格式对圣维南方程进行 图3 各分水口处ID模型解和非恒定流解的总体标准差
求解 。仿真结果如图 3所示。
［1］
总体标准差值越小，表示模型预测误差越小、预测精度越高。无论分水口位置在哪，ID 模型只
有一组预测结果，而非恒定流仿真结果与分水口的实际位置有直接关系，通过对比 ID 预测结果和同
工况下不同分水口位置的非恒定流仿真结果，计算各分水口位置工况下的总体标准差值，观察 ID 模
型预测误差的变化趋势。从图中可以看到，对于渠池 A 而言，相较于分水口位于渠池最下游端（即下
游闸前位置，x=L），ID 模型更适合预测分水口位于均匀流区和回水区交界处（即 x=L ）时的水力响应
u
过程，可将这个位置称为“ID模型最适用的分水口位置”，简称“分水口最适用点”。换言之，ID模型
关于分水口的基本假定并不合适。此时，ID 模型预测的不是分水口位于渠池下游端时渠池出、入流
增量与下游水位偏差增量的关系，而应该是分水口位于分水口最适用点时渠池出、入流增量与下游
水位偏差增量的关系。
从上面结果可以看到，在使用 ID 模型设计控制器时，如果假设分水口均位于下游端，会使得 ID
模型的预测误差较高，进而影响控制器效果。对于渠池 A 而言，均匀流区和回水区交界处为其分水
口最适用点，对于不同工程的不同渠池，该点位置可能不一样，与具体的工程物理特性、运行工况
等多因素相关，但不是本文研究重点。为简化，下述推导过程均假设均匀流区和回水区交界处为 ID
模型的分水口最适用点。

3 广义ID模型

根据上节分析可知，以 ID 模型作为预测模型时，假设分水口位于下游尾端这一做法并不合适。
只有当实际分水口恰好位于其最适用点时 ID 模型的预测精度才能最高。然而实际工程中，分水口的
位置多变，可能位于渠池的任何位置，为此需要对 ID 模型进一步修正。由此出发，考虑不同位置分
水口相对于其最适用点的分水滞后时间，使得预测模型能够尽可能达到最佳预测效果，本文提出了
如下ID修正模型，称为广义ID模型：

ì d 1 é n ù ú )
( )
)
ï e( ) t = êq 1 (t - τ - q 2 t - ∑ d i(t - τ′ i
ï dt A s ë i = 1 û
í （4）
ï L u - x i
ï τ′ i =
î c + v 0
式中：i为分水口编号；n为渠池内分水口数量；τ′ i 为 i号分水口相对于最适用点（x= L ）的分水滞后时
u
间，s；x 为 i号分水口距上游闸门距离，m。当分水口位于最适用点上游时，τ′ i 为正值，表示分水扰
i
动需要一定时间才能对下游水位产生影响；当分水口位于最适用点下游时，τ′ i 为负值，表示发生分

—600 —