Page 69 - 2022年第53卷第5期

0.16 0.15

0.14
0.12
标准化洪水过程线/h -1 0.10 标准化洪水过程线/h -1 0.10

0.08

0.06
0.04 0.05

0.02
0.00 0.00
0 50 100 150 200 250 300 0 50 100 150
时间/h 时间/h
（a） 雨峰靠后&降雨中心位于下游 （b） 雨峰靠后&降雨中心位于上游
T 1 >1&D 1 <1 （24/33场洪水） T 1 >1&D 1 >1 （9/33场洪水）
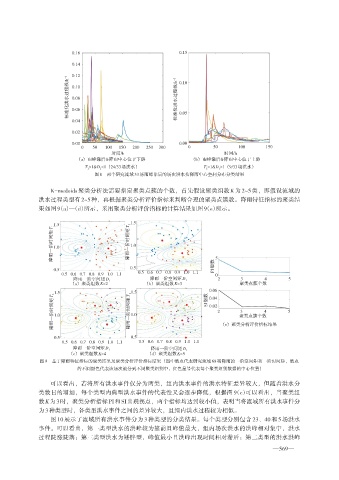
图8 两个研究流域33场雨峰靠后的场次洪水按降雨中心空间分布分类结果

K-medoids 聚类分析法需要指定聚类点簇的个数，首先假设聚类组数 K 为 2~5 类，即假设流域的
洪水过程类型有2~5种，再根据聚类分析评价指标来判断合理的聚类点簇数。降雨特征指标的聚类结
果如图9（a）—（d）所示，采用聚类分析评价指标的计算结果如图9（e）所示。

1.5
1.5
降雨一阶时间矩T 1 1.0 降雨一阶时间矩T 1 1.0

0.5 PI指数 5
0.5
0.5 0.6 0.7 0.8 0.9 1.0 1.1
0.5 0.6 0.7 0.8 0.9 1.0 1.1 0
2 3 4 5
降雨一阶空间矩D 1
降雨一阶空间矩D 1
（a） 聚类组数K=2 （b） 聚类组数K=3 聚类点簇个数
0.06
1.5 1.5 SI指数 0.04
降雨一阶时间矩T 1 1.0 降雨一阶时间矩T 1 1.0 0.02 2 （e） 聚类分析评价指标结果 5
3
4
聚类点簇个数

0.5 0.5
0.5 0.6 0.7 0.8 0.9 1.0 1.1 0.5 0.6 0.7 0.8 0.9 1.0 1.1
降雨一阶空间矩D 1
降雨一阶空间矩D 1
（c） 聚类组数K=4 （d） 聚类组数K=5
图9 基于降雨特征指标的聚类结果及聚类分析评价指标结果 （图中散点代表研究流域68场降雨的一阶空间矩和一阶时间矩，散点
的不同颜色代表该场次被分到不同聚类组别中，红色星号代表每个聚类组别数据的中心位置）

可以看出，若将所有洪水事件仅分为两类，组内洪水事件的洪水特征差异较大，但随着洪水分
类数目的增加，每个类型内典型洪水事件的代表性又会逐步降低，根据图 9（e）可以看出，当聚类组
数K为3时，聚类分析指标PI和SI出现拐点，两个指标均达到较小值，表明当将流域所有洪水事件分
为3种类型时，各类型洪水事件之间的差异较大，且组内洪水过程较为相似。
图 10 展示了流域所有洪水事件分为 3 种类型的分类结果。每个类型分别包含 23、40 和 5 场洪水
事件。可以看出，第一类型洪水的洪峰较为靠前且峰值最大，组内场次洪水的洪峰相对集中，洪水
过程陡涨陡落；第三类型洪水为矮胖型，峰值最小且洪峰出现时间相对滞后；第二类型的洪水洪峰

—569 —