Page 115 - 2022年第53卷第6期

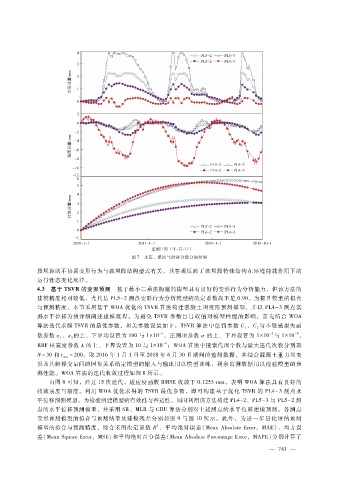
图 ７ 水压、温度与时效分量分离结果

段坝顶的不协调变形行为与该坝段结构型式有关，其客观反映了该坝段特殊结构在环境荷载作用下的
运行性态变化规律。
４．３ 基于 ＴＳＶＲ的变形预测 基于最小二乘法构建的模型具有良好的变形行为分析能力，但该方法的
建模精度相对较低，尤其是 ＰＬ５ － ２测点变形行为分析模型的决定系数尚不足 ０．９０。为提升模型的拟合
与预测精度，本节采用基于 ＷＯＡ优化的 ＴＳＶＲ算法构建混凝土坝变形预测模型，并以 ＰＬ４ － ３测点实
测水平位移为例详细阐述建模流程。为避免 ＴＳＶＲ参数盲目取值对模型性能的影响，首先结合 ＷＯＡ
算法迭代求解 ＴＳＶＲ的最优参数，相关参数设置如下：ＴＳＶＲ算法中惩罚参数 Ｃ、Ｃ与不敏感损失函
１
２
－ ８
－ ２
－ ４
的上、下界均设置为 １００与 １ × １０ ，正则项参数 σ的上、下界设置为 １ × １０ 与 １ × １０ ，
数参数 ε １ 、ε ２
－ ４
ＲＢＦ核宽度参数 λ的上、下界设置为 １０与 １ × １０ ；ＷＯＡ算法中搜索代理个数与最大迭代次数分别取
Ｎ ＝ ３０和 ｔ ＝ ２００。取 ２０１６年 １月 １日至 ２０１８年 ６月 ３０日期间的监测数据，并结合混凝土重力坝变
ｍａｘ
形及其解释变量间的因果关系给定模型的输入与输出用以模型训练，剩余监测数据用以检验模型的预
测性能。ＷＯＡ算法的迭代收敛过程如图 ８所示。
由图 ８可知，经过 １５次迭代，适应度函数 ＲＭＳＥ收敛于 ０．１２５３ｍｍ，表明 ＷＯＡ算法具有良好的
收敛速度与精度。利用 ＷＯＡ优化求得的 ＴＳＶＲ最优参数，即可构建基于优化 ＴＳＶＲ的 ＰＬ４ － ３测点水
平位移预测模型。为检验所建模型的有效性与普适性，同时利用该方法构建 ＰＬ４ － ２、ＰＬ５ － ３与 ＰＬ５ － ２测
点的水平位移预测模型，并采用 ＳＲ、ＭＬＲ与 ＧＲＵ算法分别对上述测点的水平位移建模预测。各测点
变形预测模型的拟合与预测结果及建模残差分别如图 ９与图 １０所示。此外，为进一步量化评估预测
２
模型的拟合与预测精度，综合采用决定系数 Ｒ、平均绝对误差（ＭｅａｎＡｂｓｏｌｕｔｅＥｒｒｏｒ，ＭＡＥ）、均方误
差（ＭｅａｎＳｑｕａｒｅＥｒｒｏｒ，ＭＳＥ）和平均绝对百分误差（ＭｅａｎＡｂｓｏｌｕｔｅＰｅｒｃｅｎｔａｇｅＥｒｒｏｒ，ＭＡＰＥ）分别计算了

— ７ ４ １ —