Page 125 - 2022年第53卷第6期

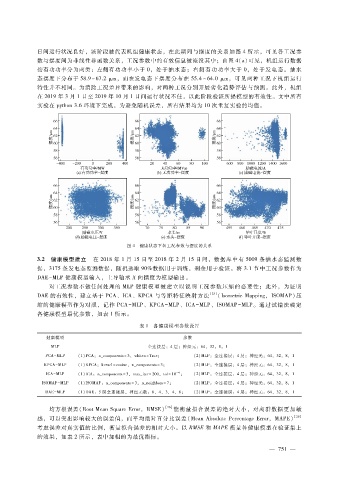
日间运行状况良好，该阶段被代表机组健康状态，在此期间与摆度的关系如图 ４所示，可见各工况参
数与摆度间为非线性非函数关系，工况参数中的有效信息被淹没其中；由图 ４（ａ）可见，机组运行数据
按有功功率分为两类：左侧有功功率小于 ０，处于抽水态；右侧有功功率大于 ０，处于发电态。抽水
态摆度下分布于 ５８．９～６７．２μ ｍ，而在发电态下摆度分布在 ５５．４～６４．０μ ｍ，可见两种工况下机组运行
特性并不相同。为消除工况差异带来的影响，对两种工况分别开展劣化趋势评估与预测。此外，机组
在 ２０１９年 ３月 １日至 ２０１９年 １０月 １日间运行状况不佳，以此阶段验证所提模型的有效性。文中所有
实验在 ｐｙｔｈｏｎ３．６环境下完成，为避免随机误差，所有结果均为 １０次重复实验的均值。

图 ４ 健康状态下各工况参数与摆度的关系
３．２ 健康模型建立 在 ２０１８年 １月 １５日至 ２０１８年 ２月 １５日间，数据库中有 ５００９条抽水态监测数
据，３１７５条发电态监测数据，随机选取 ９０％数据用于训练，剩余用于验证。将 ３．１节中工况参数作为
ＤＡＥ － ＭＬＰ健康模型输入，上导轴承 Ｘ向摆度为模型输出。
对工况参数不做任何处理的 ＭＬＰ健康模型被建立以说明工况参数压缩的必要性；此外，为证明
ＤＡＥ的有效性，建立基于 ＰＣＡ、ＩＣＡ、ＫＰＣＡ与等距特征映射方法 ［２５］ （ＩｓｏｍｅｔｒｉｃＭａｐｐｉｎｇ，ＩＳＯＭＡＰ）压
缩的健康模型作为对照，记作 ＰＣＡ － ＭＬＰ、ＫＰＣＡ － ＭＬＰ、ＩＣＡ － ＭＬＰ、ＩＳＯＭＡＰ － ＭＬＰ。通过试错法确定
各健康模型最优参数，如表 １所示。

表 １ 各健康模型参数设置

健康模型 参数
ＭＬＰ 全连接层：４层；神经元：６４，３２，８，１
ＰＣＡ － ＭＬＰ （１）ＰＣＡ：ｎ＿ｃｏｍｐｏｎｅｎｔｓ ＝ ３，ｗｈｉｔｅｎ ＝ Ｔｒｕｅ； （２）ＭＬＰ：全连接层：４层；神经元：６４，３２，８，１
ＫＰＣＡ － ＭＬＰ （１）ＫＰＣＡ：ｋｅｒｎｅｌ ＝ ｃｏｓｉｎｅ，ｎ＿ｃｏｍｐｏｎｅｎｔｓ ＝ ３； （２）ＭＬＰ：全连接层：４层；神经元：６４，３２，８，１
－ ４
ＩＣＡ － ＭＬＰ （１）ＩＣＡ：ｎ＿ｃｏｍｐｏｎｅｎｔｓ ＝ ３，ｍａｘ＿ｉｔｅｒ ＝ ２００，ｔｏｌ ＝ １０ ； （２）ＭＬＰ：全连接层：４层；神经元：６４，３２，８，１
ＩＳＯＭＡＰ － ＭＬＰ （１）ＩＳＯＭＡＰ：ｎ＿ｃｏｍｐｏｎｅｎｔｓ ＝ ３，ｎ＿ｎｅｉｇｈｂｏｒｓ ＝ ７； （２）ＭＬＰ：全连接层：４层；神经元：６４，３２，８，１
ＤＡＥ － ＭＬＰ （１）ＤＡＥ：５层全连接层，神经元数：６，４，３，４，６； （２）ＭＬＰ：全连接层：４层；神经元：６４，３２，８，１

均方根误差（ＲｏｏｔＭｅａｎＳｑｕａｒｅＥｒｒｏｒ，ＲＭＳＥ） ［２６］ 能衡量拟合误差的绝对大小，对离群数据更加敏
感，可以突出影响较大的误差值，而平均绝对百分比误差（ ＭｅａｎＡｂｓｏｌｕｔｅＰｅｒｃｅｎｔａｇｅＥｒｒｏｒ，ＭＡＰＥ） ［２６］
考虑误差对真实值的比例，衡量拟合误差的相对大小。以 ＲＭＳＥ和 ＭＡＰＥ衡量各健康模型在验证集上
的效果，如表 ２所示，表中加粗的为最优指标。

— ７ ５ １ —