Page 64 - 2022年第53卷第9期

低维多目标优化问题又适用于高维多目标优化问题。
（ ２）ＮＳＧＡ － ＩＩ通过拥挤距离来筛选同一层方案的优劣程度，当目标维度较高时，该算法的分布性
较差；因此该算法较适合于低维多目标优化问题。

４ 结果分析与讨论

４．１ 风光水多能源系统资源互补特性初步分析 风电、光电和水电出力的主要影响因素分别是风速、
太阳辐射强度和径流 ［３６］ 。根据同一研究区域内风、光和水资源的时间分布规律，可以分析得出水电出
力与风电、光电出力在年内或日内不同时间尺度上均有一定的互补性。一般而言，在年内时间尺度
上，夏季光照充足、太阳辐射强度大，汛期来水丰富、入库径流多，但风速较小；冬季太阳辐射强度
小，枯水期入库径流少，但是风速较大。在日内时间尺度上，日间太阳辐射强度大，风速较小；夜间
无光但风速较大。
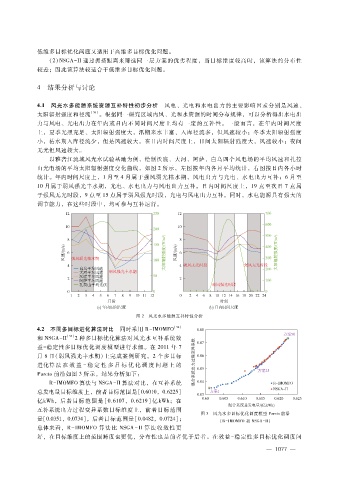
以雅砻江流域风光水试验基地为例，绘制沃底、大河、阿萨、白乌四个风电场的平均风速和扎拉
山光电场的平均太阳辐射强度变化曲线，如图 ２所示，左图按年内各月平均统计，右图按日内各小时
统计。年内时间尺度上，１月至 ４月属于强风弱光枯水期，风电出力与光电、水电出力互补；６月至
１０月属于弱风强光丰水期，光电、水电出力与风电出力互补。日内时间尺度上，１９点至次日 ７点属
于强风无光时段，９点至 １５点属于弱风强光时段，光电与风电出力互补。同时，水电能源具有强大的
调节能力，在这些时段中，均可参与互补运行。

图 ２ 风光水多能源互补特性分析

４．２ 不同多目标进化算法对比 同时采用 Ｒ － ＩＭＯＭＦＯ ［３４］
［３５］
和 ＮＳＧＡ － ＩＩ ２种多目标优化算法对风光水互补系统效
益－ 稳定性多目标优化调度模型进行求解。在 ２０１１年 ７
月 ８日（弱风强光丰水期）上完成案例研究。２个多目标
进化算 法 在 效 益 － 稳 定 性 多 目 标 优 化 调 度 问 题 上 的
Ｐａｒｅｔｏ前沿如图 ３所示，结果分析如下：
Ｒ － ＩＭＯＭＦＯ算法与 ＮＳＧＡ － ＩＩ算法对比，在互补系统
总发电量目标维度上，前者目标范围是［ ０．６０１０，０．６２２５］
亿ｋＷｈ，后者目标范围是 ［０．６１０７，０．６２１９］亿 ｋＷｈ；在
互补系统出力过程变异系数目标维度上，前者目标范围
图 ３ 风光水多目标优化调度模型 Ｐａｒｅｔｏ前沿
是［０．０３５１，０．０７３４］，后者目标范围是［０．０４８２，０．０７２４］；
（ Ｒ － ＩＭＯＭＦＯ和 ＮＳＧＡ － ＩＩ）
总体来看，Ｒ － ＩＭＯＭＦＯ算法比 ＮＳＧＡ － ＩＩ算法收敛性更
好，在目标维度上的范围跨度也更优，分布性也是前者优于后者。在效益 － 稳定性多目标优化调度问

０
— １ ７ ７ —