Page 25 - 2023年第54卷第1期
P. 25
理力学参数有很大差别;既便是岩性相同的岩体,由于各种影响因素的复杂性,其物理力学参数也会
有一定程度的变化,具有随机不确定性,对于这些随机变量可采用数理统计方法来建立相应的概率统
计模型,从整体上把握不同类型岩体力学参数的统计规律 [8] 。表 4为通过统计分析获得的软弱夹层、
无充填结构面和岩体抗剪强度参数( c、f)的概率统计模型以及相应于不同置信水平的取值范围。表中
结果表明,各类岩体的抗剪强度参数具有很强的统计规律,所获得的分布概型和相应的统计特征参数
在总体上代表了各类岩体抗剪强度参数的统计特征,同时,给出的抗剪参数取值范围可作为实际工程
中判断参数取值是否合理的重要依据。这些统计结果无论在理论和实用上都具有十分重要的价值。
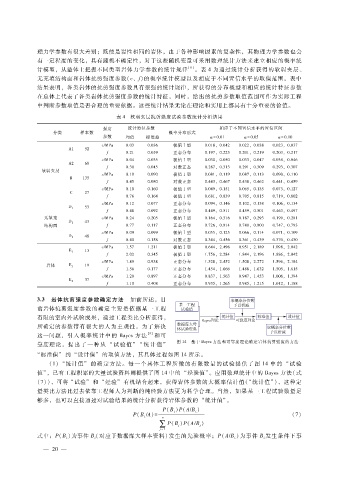
表 4 软弱夹层抗剪强度试验参数统计分析结果
强度 统计特征参数 相应于不同置信水平的置信区间
分类 样本数 概率分布形式
参数 均值 标准差 α = 0.01 α = 0.05 α = 0.10
c?MPa 0.03 0.036 极值Ⅰ型 0.018,0.042 0.022,0.038 0.023,0.037
A1 52
f 0.21 0.039 正态分布 0.197,0.223 0.201,0.219 0.203,0.217
c?MPa 0.04 0.035 极值Ⅰ型 0.030,0.050 0.033,0.047 0.034,0.046
A2 69
f 0.30 0.045 对数正态 0.287,0.313 0.291,0.309 0.293,0.307
软弱夹层
c?MPa 0.10 0.090 极值Ⅰ型 0.081,0.119 0.087,0.113 0.090,0.110
B 135
f 0.45 0.080 对数正态 0.443,0.467 0.438,0.462 0.441,0.459
c?MPa 0.10 0.160 极值Ⅰ型 0.049,0.151 0.065,0.135 0.073,0.127
C 27
f 0.76 0.164 极值Ⅰ型 0.681,0.839 0.705,0.815 0.719,0.802
c?MPa 0.12 0.077 正态分布 0.094,0.146 0.102,0.138 0.106,0.134
53
D 1
f 0.48 0.092 正态分布 0.449,0.511 0.459,0.501 0.463,0.497
无填充 c?MPa 0.24 0.205 极值Ⅰ型 0.164,0.316 0.187,0.293 0.199,0.281
43
D 2
结构面 f 0.77 0.117 正态分布 0.726,0.814 0.740,0.800 0.747,0.793
c?MPa 0.09 0.099 极值Ⅰ型 0.055,0.125 0.066,0.114 0.071,0.109
48
D 3
f 0.40 0.158 对数正态 0.344,0.456 0.361,0.439 0.370,0.430
c?MPa 1.57 1.211 极值Ⅰ型 0.644,2.496 0.951,2.189 1.098,2.042
13
E 2
f 2.02 0.345 极值Ⅰ型 1.756,2.284 1.844,2.196 1.886,2.042
c?MPa 1.89 0.938 正态分布 1.328,2.452 1.508,2.272 1.596,2.184
岩体 E 3 19
f 1.56 0.177 正态分布 1.454,1.666 1.488,1.632 1.505,1.615
c?MPa 1.20 0.897 正态分布 0.837,1.563 0.947,1.453 1.006,1.394
37
E 4
f 1.10 0.408 正态分布 0.935,1.265 0.985,1.215 1.012,1.188
3.3 岩体抗剪强度参数确定方法 如前所述,目
前岩体抗剪强度参数的确定主要是依据某一工程
有限的室内外试验成果,通过工程类比分析获得,
所确定的参数带有很大的人为主观性。为了解决
这一问题,引入概率统计中的 Bayes方法 [9] 和可
图 14 基于 Bayes方法和可靠度理论确定岩体抗剪强度的方法
靠度理 论,提 出 了 一 种 从 “试 验 值 ” “统 计 值 ”
“标准值” 到 “设计值” 的取值方法,其具体过程如图 14所示。
(1) “统计值” 的确定方法。每一个具体工程所做的有限数量的 试验 提供 了 图 14中的 “试验
值”,已有工程积累的大量试验资料则提供了图 14中的 “经验值”。应用数理统计中的 Bayes方法(式
( 7)),可将 “试验” 和 “经验” 有机结合起来,获得岩体参数的大概率估计值(“统计值”),这种定
量类比方法比过去依靠工程师人为判断的纯经验方法更为科学合理。当然,如果某一工程试验数量足
够多,也可以直接通过对试验结果的统计分析获得岩体参数的 “统计值”。
P(B)P(A?B)
P(B?A) = n i i (7)
i
∑ P(B)P(A?B)
j
j
j =1
式中:P(B)为事件 B(对应于数据库大样本资料)发生的先验概率;P(A?B)为事件 B发生条件下事
i i i i
— 2 0 —