Page 101 - 2023年第54卷第4期
P. 101
N(t),则冰层厚度计算式:
k Nt= ρ i k i k
会发生堆积、增厚。由 M = ρ i k i 0
N ) (5)
( t) = M ?( ρ i max
i k k
2.4 初始条件及边界条件 模型的初始条件包括计算单元节点上的流量和水位。根据水动力学模型计
算初始时刻上游流量及下游对应水位下每一个单元节点上的流量及水位,得到某一初始时刻流量和水
位下模型的初始条件。
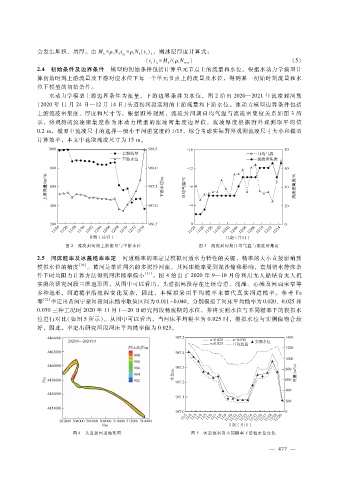
水动力学模型上游边界条件为流量,下游边界条件为水位,图 2给出 2020—2021年流凌封河期
( 2020年 11月 24日—12月 14日)头道拐河段实测的上游流量和下游水位。冰动力模型边界条件包括
上游流凌密集度、厚度和尺寸等。根据野外观测,流凌封河期日均气温与流凌密集度关系如图 3所
示,将观测的流凌密 集度 作为 冰动力 模型 的流凌 密 集 度 边 界 值,流 凌 厚 度 根 据 野 外 观 测 取 平 均 值
0.2m,模型中流凌尺寸的选择一般小于河道宽度的 1?15,综合考虑实际野外观测流凌尺寸大小和模型
计算效率,本文中选取流凌尺寸为 15m。
图 2 流凌封河期上游流量与下游水位 图 3 流凌封河期日均气温与流凌密集度
2.5 河床糙率及冰盖糙率率定 河道糙率的率定是模拟河道水力特性的关键,糙率的大小直接影响到
模拟水位的精度 [20] 。黄河是举世闻名的多泥沙河流,其河床糙率受到泥沙输移影响,套用清水静床条
件下时均阻力计算方法得到河床糙率偏小 [21] 。图 4给出了 2020年 9—10月份利用无人船结合无人机
实测的研究河段三维地形图,从图中可以看出,头道拐河段存在连续弯道、浅滩、心滩及河面束窄等
多种地形,河道糙率沿流 程 变 化 复 杂,因 此,本 模 拟 采 用 平 均 糙 率 来 替 代 真 实 河 道 糙 率。参 考 Fu
等 [22] 率定出黄河宁蒙河段河床糙率取值区间为 0.011~0.040,分别模拟了河床平均糙率为 0.020、0.025和
0.030三种工况时 2020年 11月 1—20日研究河段畅流期的水位,并将实测水位与不同糙率下的模拟水
位进行对比(如图 5所示)。从图中可以看出,当河床平均糙率为 0.025时,模拟水位与实测值吻合较
好,因此,率定出研究河段河床平均糙率值为 0.025。
图 4 头道拐河道地形图 图 5 河道流量及不同糙率下沿程水位变化
— 4 7 7 —