Page 40 - 2023年第54卷第7期

注：ｎ?ｎ ０ 为单位转速相对值；ｑ?ｑ ０ 为单位流量相对值；Ｅ?Ｅ ０ 为效率相对值；Ｔ?Ｔ ０ 为扭矩相对值。
图 ５ 飞逸过程外特性参数变化

４．２ 内流场分析 以上结果表明，水轮机内的效率逐渐下降为零，而效率的变化与转轮内部流态紧密
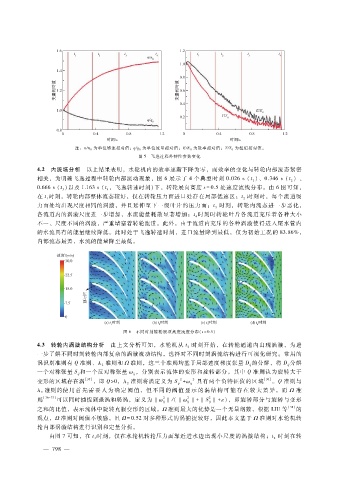
相关，为明确飞逸过程中转轮内部流动现象，图 ６展示了 ４个典型时刻 ０．０２６ｓ（ｔ）、０．３４６ｓ（ｔ）、
２
１
０．６６６ｓ（ｔ）以及 １．１６３ｓ（ｔ，飞逸转速时刻）下，转轮展向高度 ｓ ＝ ０．５ 处速度流线分布。由 ６图可知，
３ ４
在 ｔ时刻，转轮内部整体流态较好，仅在转轮压力面进口处存在局部低速区；ｔ时刻时，每个流道吸
１ ２
力面处均出现尺度相同的涡漩，并且延伸至下一级叶片的压力面；ｔ时刻，转轮内流态进一步恶化，
３
各流道内的涡漩尺度进一步增加，水流能量耗散显著增加；ｔ时刻时转轮叶片各流道充斥着各种大小
４
不一、尺度不同的涡漩，严重堵塞着转轮流道。此外，由于流道内充斥的各种涡漩使得进入尾水管内
的水流具有的能量继续降低。此时处于飞逸转速时刻，进口流量降到最低，仅为初始工况的 ８３．８６％，
内部流态最差，水流的能量降至最低。

图 ６ 不同时刻转轮展项高度速度分布（ｓ ＝ ０．５ ）

４．３ 转轮内涡漩结构分析 由上文分析可知，水轮机从 ｔ时刻开始，在转轮通道内出现涡漩，为进
２
一步了解不同时刻转轮内部复杂的涡漩流动结构，选择对不同时刻涡流结构进行可视化研究。常用的
准则和 Ω准则，这三个准则均基于局部速度梯度张量 Ｄ 的分解，将 Ｄ 分解
涡识别准则有 Ｑ准则、λ ２
ｉｊ ｉｊ
，分别表示流体的变形和旋转部分。其中 Ｑ准则认为旋转大于
ｉｊ
一个对称张量 Ｓ和一个反对称张量 ω ｉｊ
２
变形的区域存在涡 ［３５］ ，即 Ｑ＞０，λ ２ 准则将涡定义为 Ｓ ＋ ω ｉｊ ２ 具有两个负特征值的区域 ［３６］ 。Ｑ准则与
ｉｊ
准则的使 用 首 先 需 要 人 为 确 定 阈 值，但 不 同 的 阈 值 显 示 的 涡 结 构 可 能 存 在 较 大 差 异。而 Ω准
λ ２
２
２
２
则 ［３６ － ３７］ 可以同时捕捉到强涡和弱涡，定义为‖ω ｉｊ ‖?（ ‖ω ｉｊ ‖ ＋ ‖Ｓ‖ ＋ ε ），即旋转部分与旋转与变形
ｉｊ
之和的比值，表示流体中旋转克服变形的区域。Ω准则最大的优势是一个无量纲数，根据 ＬＩＵ等 ［３８］ 的
观点，Ω准则对阈值不敏感，且 Ω ＝ ０．５２ 对多种形式的涡捕捉较好，因此本文基于 Ω准则对水轮机转
轮内部涡漩结构进行识别和定量分析。
由图 ７可知，在 ｔ时刻，仅在水轮机转轮压力面靠近进水边出现小尺度的涡漩结构；ｔ时刻在转
１ ２
８
— ７ ９ —