Page 124 - 2023年第54卷第8期

式中：Ｘ 为归一化后的数据；Ｘ 、Ｘ 分别为样本的最大值、最小值。
ｎｏｒｍ ｍａｘ ｍｉｎ
２．２．２ 模型的构建 本文构建的 ＡＮＮ模型包括输入层、隐层、输出层三层，以枝城站作为上断面，
即枝城站的流量 Ｑ、含沙量 Ｓ为模型输入层，将荆南三口概化为下断面，荆南三口的流量（即为三口 ５
个水文站流量之和）Ｑ、含沙量 Ｓ为输出层。隐层主要是用来将输入数据映射到输出空间，对于隐层节
点数的确定目前尚无成熟的理论方法，常采用已有的经验公式来确定隐含层节点数，本模型采用了
Ｈｅｃｈｔ － Ｎｉｅｌｓｅｎ＆ Ｉｌｌｉｎｇｗｏｒｔｈ ［２４］ 公式：ｈ ＝ ４ Ｎ，Ｎ为输入层节点数，因此，隐含层节点数设置为 ８。本模
型输入层与输出层之间的关系为：
ｎ
ｘ －
∑
ｙ ＝ ｆ（ ω ｉ ｉ θ ） （２）
ｉ ＝１
为第 ｉ个神经元的连接权重；ｘ为输入的神经元；θ 为阈值，初始值取 ０．１；ｎ为输入神经元
式中：ω ｉ ｉ
个数。
在神经网络中，输出层都是输入层的线性组合，为了加入非线性元素，常引入激活函数。ＡＮＮ常
见的激活函数有 Ｓｉｇｍｏｉｄ、ｔａｎｈ、ＲｅＬｕ等 ［２５］ ，本模型在计算过程中采用了相对于 Ｓｉｇｍｏｉｄ和 ｔａｎｈ有更
快收敛速度且不会出现梯度消失问题的 ＲｅＬｕ函数。
ＡＮＮ模型的拟合精度通过损失函数来体现，拟合精度为 １与损失函数值的差值，本模型在构建时
采用的损失函数为均方误差（ ＭＳＥ），函数表达式为：
ｍ
∑ （ｙ－ ｙ） ２
ｉ
ｉ ＝１
ＭＳＥ ＝ （３）
ｍ
式中：ｙ为三口分流量计算值；ｙ为实际值；ｍ为样本个数。
ｉ

３ 荆南三口实测分流分沙变化

从 １９５０年代以来，荆江河段先后经历了下荆江裁弯、葛洲坝修建、三峡水库蓄水和长江上游梯
级电站的修建与运行等，这些人类活动均会导致来水来沙量发生变化。以下主要分析 １９９１—２０２０年
段枝城站及荆南三口水沙变化情况。
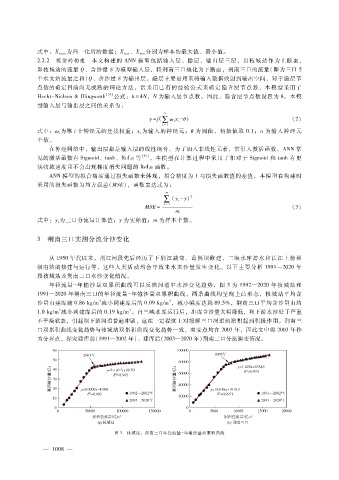
年径流量 － 年输沙量双累积曲线可以反映河道中水沙变化趋势，图 ３为 １９９２—２０２０年枝城站和
１９９１—２０２０年荆南三口的年径流量－ 年输沙量双累积曲线，两条曲线均呈现上凸形态，枝城站平均含
３
３
沙量由建库前 ０．８６ｋｇ?ｍ 减小到建库后的 ０．０９ｋｇ?ｍ ，减小幅度达到 ８９．５％，荆南三口平均含沙量由约
３
３
１．０ｋｇ?ｍ 减小到建库后的 ０．１９ｋｇ?ｍ 。自三峡水库运行后，出库含沙量大幅降低，坝下游水沙处于严重
不平衡状态，引起坝下游河道普遍冲刷，这在一定程度上对缓解三口河道的淤积起到积极作用。荆南三
口双累积曲线变化趋势与枝城站双累积曲线变化趋势一致，突变点均在 ２００３年，因此文中将 ２００３年作
为分界点，探究建库前（１９９１—２００２年）、建库后（２００３—２０２０年）荆南三口分流演变情况。

图 ３ 枝城站、荆南三口年径流量－ 年输沙量双累积曲线

— １ ０ ８ —
０