Page 95 - 2023年第54卷第8期

型以优化装机，研究表明风电和光伏的最优装机差异较大。Ｆａｎｇ等 ［１７］ 通过最大化全生命周期的净收
入，提出了一种集成到水电站中的光伏电站优化装机容量的方法，研究选择目前世界上规模最大的龙
羊峡水电－ 光伏发电项目作为案例，计算了不同出力情景下的最优光伏装机容量。Ｍｉｎｇ等 ［１８］ 提出了一
个同步确定水光系统光伏容量和长期运行规则的框架，实例研究验证了该框架的有效性。Ｙａｎｇ等 ［１９］
开发了一个气候水文运行框架，确定在气候变化条件下适合并入水电系统的光伏电站容量，研究表明
在一定的装机容量范围内互补系统有良好的适应气候变化的运行能力。
然而，以往的研究方法计算过程复杂，难以明晰经济技术参数与最优装机容量和互补系统净效益
之间关系，而解析优化方法只需获取少量参数即可进行容量配置，并能够量化最优装机、互补系统净
效益对上网电价、装机成本等各经济技术参数的敏感性，有助于明确装机规划中各要素之间关系，为
未来经济技术参数变化情形提供装机规划调整策略。
鉴于上述问题，本文耦合短期弃电规律、中长期优化调度、成本 － 效益分析模型，提出了一种装
机容量配置解析优化方法，定量分析装机规划与经济技术因素内外两方面对系统总效益影响。首先，
建立耦合短期弃电的中长期优化调度模型求解风光弃电率函数；其次，解析基于该函数的成本 － 效益
模型推求最优装机函数，并与数值模拟方法比较以检验合理性；最后，进一步解析最优装机函数分析
装机规划中的各经济技术参数敏感性。以雅砻江流域二滩水电站及周边风光系统为研究对象，检验所
构建解析优化方法的可行性和合理性。

２ 研究方法

２．１ 风光弃电率函数 和传统水电站存在弃水类似，水风光互补电站中普遍存在弃风、弃光的情况。
当互补系统的出力大于该时刻负荷需求，或超出了电网输送能力就会产生弃电。由于风电、光伏功率
与装机容量成线性关系 ［２０］ ，扩大风光装机规模会使实际风光出力也相应地线性增加，在水电调节能力
有限的情况下风电弃电率、光伏弃电率也会相应提高，因此本研究做出假设：在一定装机范围内，风
电多年平均弃电率与风电装机呈线性，光伏多年平均弃电率与光伏装机呈线性。
{ γ ｗ ＝ ｋＩ＋ ｃ Ｉ，Ｉ ∈ ［Ｉ ，Ｉ ］ （１）
１ ｗ
１
ｓ
ｗ
ｍａｘ
ｍｉｎ
２ ｓ
γ ｓ ＝ ｋＩ ＋ ｃ
２
为风电、光伏多年平均弃电率；Ｉ、Ｉ为风电装机、光伏装机容量，ＭＷ；Ｉ 、Ｉ 为装
ｗ ｓ ｍｉｎ ｍａｘ
式中：γ ｗ 、γ ｓ
机容量下、上限值；ｋ、ｋ、ｃ、ｃ为弃电率函数系数。求解风光弃电率函数包括以下三个步骤。
１
１
２
２
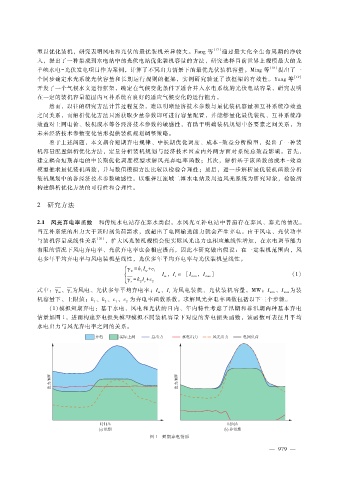
（ １）模拟短期弃电：基于水电、风电和光伏的日内、年内特性考虑了汛期和非汛期两种基本弃电
情景如图 １，进而构建弃电损失模型模拟不同装机容量下对应的弃电损失函数，该函数可表征月平均
水电出力与风光弃电率之间的关系。

图 １ 短期弃电情形

— ９ ７ ９ —