Page 100 - 2024年第55卷第5期

连续级配方程有 ３个参数，分别为 ｄ 、ａ和 ｎ。最大粒径 ｄ 是土体的固有属性，可以直接量测
ｍａｘ ｍａｘ
确定。ａ和 ｎ可 通 过 基 于 Ｌｅｖｅｒｎｂｅｒｇ － Ｍａｒｑｕａｒｄｔ算 法 的 非 线 性 最 小 二 乘 法 拟 合 得 到， Ｌｅｖｅｒｎｂｅｒｇ －
Ｍａｒｑｕａｒｄｔ 算法是介于牛顿法与梯度下降法之间的一种非线性优化方法，既有牛顿法的收敛速度又有梯
度下降法的收敛性能 ［２９］ 。
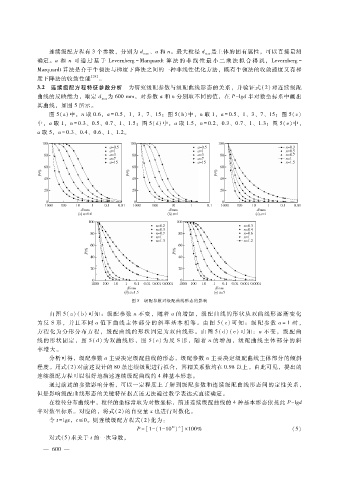
３．２ 连续级配方程特征参数分析 为研究级配参数与级配曲线形态的关系，并验证式（２）对连续级配
曲线的反映能力，取定 ｄ 为 ６００ｍｍ，对参数 ａ和 ｎ分别取不同的值，在 Ｐ － ｌｇ ｄ半对数坐标系中画出
ｍａｘ
其曲线，如图 ５所示。
图 ５（ａ）中，ｎ取 ０．６，ａ ＝ ０．５ 、１、３、７、１５；图 ５（ｂ）中，ｎ取 １，ａ ＝ ０．５ 、１、３、７、１５；图 ５（ｃ）
中，ａ取 １，ｎ ＝ ０．３ 、０．５、０．７、１、１．５；图 ５（ｄ）中，ａ取 １．５，ｎ ＝ ０．２ 、０．３、０．７、１、１．３；图 ５（ｅ）中，
ａ取 ５，ｎ ＝ ０．３、０．４、０．６、１、１．２。

图 ５ 级配参数对级配曲线形态的影响
由 图 ５（ａ）（ｂ）可知：级配参数 ｎ不变，随着 ａ的增加，级配曲线的形状从双曲线形逐渐变化
为反 Ｓ形，并且不同 ａ值下曲线 主 体 部 分 的 斜 率 基 本 相 等。 由 图 ５（ｃ）可 知： 级 配 参 数 ａ ＝ １时，
方程化为分形分布方程，级配曲线的形状固定为双曲线形。由图 ５（ｄ）（ｅ）可知：ａ不 变， 级 配 曲
线的形状固定，图 ５（ｄ）为双曲线形，图 ５（ｅ）为反 Ｓ形，随着 ｎ的增加，级配曲线 主 体 部 分 的 斜
率增大。
分析可得，级配参数 ａ主要决定级配曲线的形态，级配参数 ｎ主要决定级配曲线主体部分的倾斜
程度。用式（２）对前述设计的 ８０条连续级配进行拟合，其相关系数均在 ０．９８以上。由此可见，提出的
连续级配方程可以很好地描述连续级配曲线的 ４种基本形态。
通过前述的参数影响分析，可以一定程度上了解到级配参数和连续级配曲线形态间的定性关系，
但是影响级配曲线形态的关键特征拐点还无法通过数学表达式直接确定。
在粒径分布曲线中，粒径的坐标常取为对数坐标，前述连续级配曲线的 ４种基本形态依托此 Ｐ － ｌｇ ｄ
半对数坐标系。对应的，将式（２）的自变量 ｘ也进行对数化。
令 ｔ ＝ ｌｇ ｘ，ｔ ≤０。则连续级配方程式（２）化为：
ｎｔ ａ
Ｐ ＝ ［１ － （１ － １０ ）］ × １００ ％ （５）
对式（５）求关于 ｔ的一次导数，

０
— ６ ０ —