Page 101 - 2024年第55卷第5期

ｎｔ
ｎｔ ａ － １
Ｐ′ ＝ ｌｎ１０ａｎ１０（１ － １０ ） （６）
对式（ ５）求关于 ｔ的二次导数，
２
ｎｔ ａ － ２
ｎｔ
２
ｎｔ
Ｐ″ ＝ ｌｎ１０ａｎ１０（１ － １０ ） （１ － ａ１０ ） （７）
ｎｔ
２
２
ｎｔ
ｎｔ ａ － ２
式中 ｌｎ１０ａｎ１０（１ － １０ ） ＞０。因此，１ － ａ１０ 决定 Ｐ″的正负。
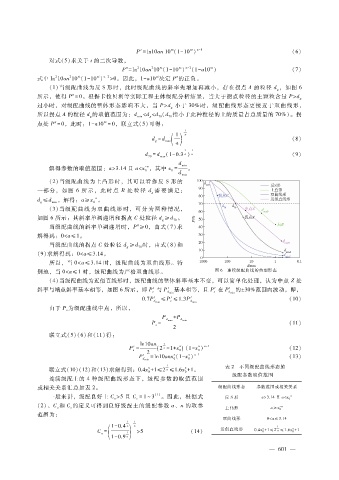
（ １）当级配曲线为反 Ｓ形时，此时级配曲线的斜率先增加再减小，存在拐点 Ａ的粒径 ｄ，如图 ６
ｇ
所示，使得 Ｐ″ ＝ ０。根据卡拉贝利等实际工程土体级配分析结果，当大于拐点粒径的土颗粒含量 Ｐ＞ｄ
ｇ
过小时，对级配曲线的整体形态影响不大，当 Ｐ＞ｄ 小于 ３０％时，级配曲线形态更接近于双曲线形，
ｇ
所以拐点 Ａ的粒径 ｄ的取值范围为：ｄ ＜ｄ＜ｄ （ｄ 指小于此种粒径的土的质量占总质量的 ７０％）。拐
ｇ ｍｉｎ ｇ ７０ ７０
ｎｔ
点处 Ｐ″ ＝ ０，此时：１ － ａ１０ ＝ ０，联立式（５）可得：
１
１
ｄ＝ ｄ ( ) ｎ （８）
ｇ ｍａｘ ａ
１ １
ｄ ＝ ｄ （１ － ０．３ ａ ） ｎ （９）
７０
ｍａｘ
ｄ ｍｉｎ
－ ｎ
解得参数的取值范围：ａ＞３．１４且 ａ＜ｘ ，其中 ｘ＝ 。
０ ０
ｄ
ｍａｘ
（２）当级配曲线为上凸形时，其可以看作反 Ｓ形的
一部分，如 图 ６所 示，此 时 点 Ｂ处 粒 径 ｄ需 要 满 足：
ｇ
－ ｎ
ｄ≤ｄ ，解得：ａ ≥ｘ 。
ｍｉｎ
ｇ
０
（ ３）当级配 曲 线 为 双 曲 线 形 时，可 分 为 两 种 情 况，
如图 ６所示：其斜率单调递增和拐点 Ｃ处粒径 ｄ≥ｄ 。
７０
ｇ
当级配曲线的斜率单调递增时，Ｐ″ ≥０，由式（７）求
解得到：０＜ａ ≤１。
当级配曲线的拐点 Ｃ处粒径 ｄ≥ｄ 时，由式（８）和
ｇ ７０
（ ９）求解得到：０＜ａ ≤３．１４。
所以，当 ０＜ａ ≤３．１４时，级配曲线为双曲线形。特
别地，当 ０＜ａ ≤１时，级配曲线为严格双曲线形。 图 ６ 连续级配曲线的典型形态
（４）当级配曲线为近似直线形时，级配曲线的整体斜率基本不变，可以简单化处理，认为中点 Ｚ处
斜率与端点斜率基本相等，如图 ６所示，即 Ｐ′与 Ｐ′ 基本相等，且 Ｐ′在 Ｐ′ 的±３０％范围内波动，即，
ｚ
ｚ
ｄ ｍｉｎ
ｄ ｍｉｎ
０．７Ｐ′ ≤Ｐ′ ≤１．３Ｐ′ （１０）
ｄ ｍｉｎ ｚ ｄ ｍｉｎ
由于 Ｐ为级配曲线中点，所以，
ｚ
Ｐ ＋ Ｐ
ｄ ｍａｘ ｄ ｍｉｎ
Ｐ＝ （１１）
ｚ
２
联立式（ ５）（６）和（１１）得：
ｌｎ１０ ａｎ １
Ｐ′ ＝ ( ｎ ｎ ａ － １ （１２）
２ ａ－ １ ＋ ｘ) （１ － ｘ）
ｚ ０ ０
２
ｎ ａ － １
ｎ
Ｐ′ ＝ ｌｎ１０ ａｎｘ（１ － ｘ） （１３）
ｄ ｍｉｎ ０ ０
１
ｎ ｎ 表 ２ 不同级配曲线形态的
联立式（１０）（１２）和（１３）求解得到：０．４ｘ＋ １ ≤２ ａ ≤１．６ｘ＋ １ 。
０ ０
级配参数取值范围
连续级配土的 ４种级配曲线形态下，级配参数的取值范围
或相关关系汇总如表 ２。 级配曲线形态 参数范围或相关关系
［１］
一般来讲，级配良好土 Ｃ＞５且 Ｃ ＝ １～３ 。因此，根据式 反 Ｓ形 － ｎ
ｕ ｃ ａ＞３．１４且 ａ＜ｘ ０
（ ２）、Ｃ和 Ｃ的定义可得到良好级配土的级配参数 ａ、ｎ的取参 － ｎ
ｕ ｃ 上凸形 ａ ≥ｘ ０
范围为：
双曲线形 ０＜ａ ≤３．１４
１ １
( １ － ０．４ ａ ｎ 近似直线形 ０．４ｘ ０ １ ≤２ ａ≤１．６ｘ ０ １
１
ｎ
ｎ
＋
＋
Ｃ ＝ １ － ０．９ ａ) ＞５ （１４）
ｕ １
— ６ ０ １ —