Page 99 - 2024年第55卷第5期

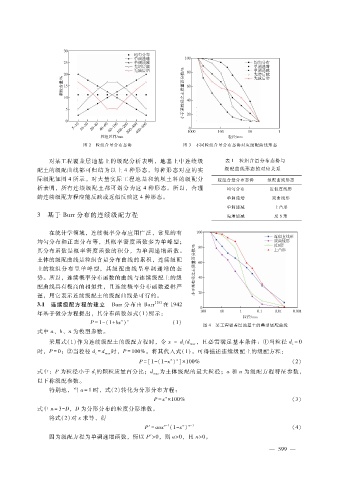
图 ２ 粒组含量分布态势 图 ３ 不同粒组含量分布态势对应级配曲线形态

对某工程覆盖层地基土的级配分析表明，地基土中连续级 表 １ 粒组含量分布态势与
配土的级配曲线都可归结为以上 ４种形态，每种形态对应的实 级配曲线形态的对应关系
际级配如图 ４所示。对大量实际工程地基和筑坝土料的级配分 粒组含量分布态势 级配曲线形态
析表明，所有连续级配土都可划分为这 ４种形态。所以，合理 均匀分布 近似直线形
的连续级配方程应能反映或近似反映这 ４种形态。 单调递增 双曲线形
单调递减 上凸形
３ 基于 Ｂｕｒｒ分布的连续级配方程 先增后减 反 Ｓ形

在统计学领域，连续概率分布应用广泛，常见的有
均匀分布和正态分布等，其概率密度函数多为单峰型；
其分布函数是概率密度函数的积分，为单调递增函数。
土体的级配曲线是粒组含量分布曲线的累积，连续级配
土的粒组 分 布 呈 单 峰 型，其 级 配 曲 线 呈 单 调 递 增 的 态
势。所以，连续概率分布函数的曲线与连续级配土的级
配曲线具有极高的相似性，且连续概率分布函数逻辑严
谨，用它表示连续级配土的级配曲线是可行的。
［２８］
３．１ 连续级配方程的建立 Ｂｕｒｒ分布由 Ｂｕｒｒ 在 １９４２
年基于微分方程提出，其分布函数如式（１）所示：
ｎ ａ
Ｐ ＝ １ － （１ ＋ ｂｘ） （１）
图 ４ 某工程覆盖层地基土的典型级配曲线
式中 ａ、ｂ、ｎ为模型参数。
采用式（１）作为连续级配土的级配方程时，令 ｘ＝ｄ?ｄ ，且必需满足基本条件：①当粒径 ｄ＝ ０
ｉ ｍａｘ ｉ
时，Ｐ ＝ ０ ；②当粒径 ｄ＝ ｄ 时，Ｐ ＝ １００％。将其代入式（１），可得描述连续级配土的级配方程：
ｉ ｍａｘ
ｎ ａ
Ｐ ＝ ［１ － （１ － ｘ）］ × １００ ％ （２）
式中：Ｐ为粒径小于 ｄ的颗粒质量百分比；ｄ 为土体级配的最大粒径；ａ和 ｎ为级配方程特征参数，
ｉ ｍａｘ
以下称级配参数。
特别地，当 ａ ＝ １时，式（２）转化为分形分布方程：
ｎ
Ｐ ＝ ｘ× １００ ％ （３）
式中 ｎ ＝ ３ － Ｄ，Ｄ为分形分布的粒度分形维数。
将式（ ２）对 ｘ求导，得
ｎ ａ － １
ｎ － １
Ｐ′ ＝ ａｎｘ （１ － ｘ） （４）
因为级配方程为单调递增函数，所以 Ｐ′＞０，则 ａ＞０，且 ｎ＞０。
— ５ ９ ９ —