Page 129 - 2025年第56卷第1期

测值。 综上所述， ＡＣＧＷＯ－ＲＦ 算法能够代替传
统算法进行碾压质量评价， 具有适用性。
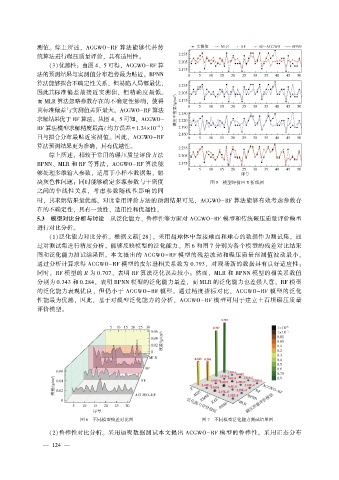
（３）优越性： 由图 ４、 ５ 可得， ＡＣＧＷＯ－ＲＦ 算
法的预测结果与实测值分布趋势最为贴近。 ＢＰＮＮ
算法能够拟合不确定性关系， 但易陷入局部最优，
因此其标准偏差最接近实测值， 但精确度最低。
而 ＭＬＲ 算法忽略参数存在的不确定性影响， 使得
其标准偏差与实测值差距最大。 ＡＣＧＷＯ－ＲＦ 算法

求解结果优于 ＲＦ 算法。 从图 ４、 ５ 可知， ＡＣＧＷＯ－
－４
ＲＦ 算法模型求解精度最高（均方误差 ＝ １．２４×１０ ）
且与拟合分布最贴近实测值。 因此， ＡＣＧＷＯ－ＲＦ
算法预测结果更为准确， 具有优越性。
综上所述， 相较于常用的碾压质量评价方法
ＢＰＮＮ、 ＭＬＲ 和 ＲＦ 等算法， ＡＣＧＷＯ－ＲＦ 算法能
够处理多维输入参数， 适用于小样本数据集， 解
决灰色性问题； 同时能够确定多源参数与干密度 图 ５ 模型评价四 Ｙ 折线图
之间的非线性关系， 考虑参数随机性影响的同
时， 其求解结果最优越。 对比常用评价方法的预测结果可见， ＡＣＧＷＯ－ＲＦ 算法能够有效考虑参数存

在的不确定性， 具有一致性、 适用性和优越性。
５．３ 模型对比分析与讨论 从泛化能力、 鲁棒性等方面对 ＡＣＧＷＯ－ＲＦ 模型和传统碾压质量评价模型

进行对比分析。
（１）泛化能力对比分析。 根据文献［２８］， 采用超球体中靠接球面和球心的数据作为测试集， 通
过对测试集进行精度分析， 能够反映模型的泛化能力。 图 ６ 和图 ７ 分别为各个模型的残差对比结果

图和泛化能力测试结果图。 本文提出的 ＡＣＧＷＯ－ＲＦ 模型的残差波动和碾压质量预测值波动最小。
通过分析计算求得 ＡＣＧＷＯ－ＲＦ 模型的皮尔逊相关系数为 ０．７９３， 对现场新的数据具有良好适应性；
同时， ＲＦ 模型的 Ｒ 为 ０．７０７， 表明 ＲＦ 算法泛化误差较小； 然而， ＭＬＲ 和 ＢＰＮＮ 模型的相关系数值
分别为 ０．３４３ 和 ０．２８４， 表明 ＢＰＮＮ 模型的泛化能力最差， 而 ＭＬＲ 的泛化能力也差强人意， ＲＦ 模型
的泛化能力表现优良， 但仍小于 ＡＣＧＷＯ－ＲＦ 模型。 通过精度指标对比， ＡＣＧＷＯ－ＲＦ 模型的泛化
性能最为优越， 因此， 基于对模型泛化能力的分析， ＡＣＧＷＯ－ＲＦ 模型可用于建立土石坝碾压质量

评价模型。

图 ６ 不同模型残差对比图 图 ７ 不同模型泛化能力测试结果图

（２）鲁棒性对比分析。 采用加噪数据测试本文提出 ＡＣＧＷＯ－ＲＦ 模型的鲁棒性。 采用正态分布

— １ ２ ４ —