Page 130 - 2025年第56卷第1期

生成随机噪声值附加在已有的训练数据集中的含
水率和 Ｐ５ 含量上， 通过在不同方差噪声下模型
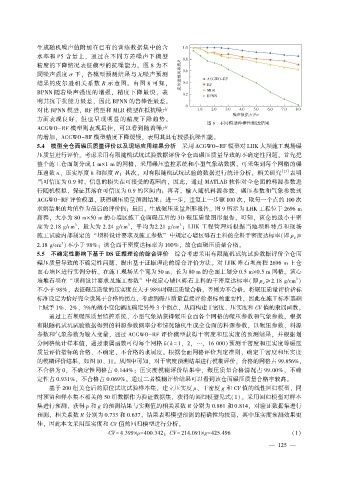
精度的下降情况表征模型的抗噪能力。 图 ８ 为不
同噪声强度 σ 下， 各模型预测结果与无噪声预测
结果的皮尔逊相关系数 Ｒ 示意图。 由图 ８ 可知，
ＢＰＮＮ 随着噪声强度的增强， 精度下降最快， 表
明其抗干扰能力最差， 因此 ＢＰＮＮ 的鲁棒性最差。
对比 ＢＰＮＮ 模型， ＲＦ 模型和 ＭＬＲ 模型在抵抗噪声

方面表现良好， 但也呈现明显的精度下降趋势。
图 ８ 不同模型鲁棒性测试结果
ＡＣＧＷＯ－ＲＦ 模型则表现最佳， 可以看到随着噪声
的增加， ＡＣＧＷＯ－ＲＦ 模型精度下降缓慢， 表明其具有较强抗噪性能。
５．４ 模型全仓面碾压质量评价以及现场应用结果分析 采用 ＡＣＧＷＯ－ＲＦ 模型对 ＬＨＫ 大坝施工现场碾
压质量进行评价。 考虑采用有限随机试坑试验数据评价全仓面碾压质量导致的不确定性问题， 首先把
整个施工仓面划分成 １ ｍ×１ ｍ 的网格， 采用碾压监控系统和小型气象站数据， 可采集到每个网格的碾
压遍数 ｎ、 压实厚度 ｈ 和湿度 Ｈ； 其次， 对有限随机试坑试验的数据进行统计分析， 相关研究 ［１３］ 表明
当可信度为 ０．９ 时， 信息的损失在可接受的范围内， 因此， 通过 ＭＡＴＬＡＢ 软件对全仓面的料源参数进
行随机模拟， 保证其落在可信度为 ０．９ 的区间内； 再者， 输入随机料源参数、 碾压参数和气象参数到
ＡＣＧＷＯ－ＲＦ 评价模型， 获得碾压质量预测结果； 进一步， 重复上一步骤 １００ 次， 取每一个点的 １００ 次

求解结果的均值作为最后的评价值； 最后， 生成碾压质量图形报告。 图 ９ 所示为 ＬＨＫ 工程位于 ２６９６ ｍ
高程， 大小为 ８０ ｍ×５０ ｍ 的心墙区施工仓面碾压后的 ３Ｄ 碾压质量图形报告， 可知， 该仓的最小干密
度为 ２．１８ ｇ∕ｃｍ ， 最大为 ２．２４ ｇ∕ｃｍ ， 平均为２．２１ ｇ∕ｃｍ ； ＬＨＫ 工程管理局根据当地坝料特点和现场
３
３
３
施工试验内部制定的 “坝料设计要求及施工参数” 中规定心墙区砾石土料的全料干密度达标率（即 ρ ≥
ｄ
３
２．１８ ｇ∕ｃｍ ）不小于 ９８％； 该仓面干密度达标率为 １００％， 故仓面碾压质量合格。
５．５ 不确定性影响下基于 ＤＳ 证据理论的综合评价 综合考虑采用有限随机试坑试验数据评价全仓面
碾压质量导致的不确定性问题， 提出基于证据理论的综合评价方法。 对 ＬＨＫ 堆石坝高程 ２６９６ ｍ 上仓
面心墙区进行实例分析。 在施工现场某个宽为 ５０ ｍ、 长为 ８０ ｍ 的仓面上划分 ０．５ ｍ×０．５ ｍ 网格。 该心
３
墙堆石坝在 “坝料设计要求及施工参数” 中规定心墙区砾石土料的干密度达标率（即 ρ ≥２．１８ ｇ∕ｃｍ ）
ｄ
不小于 ９８％， 表征碾压质量的压实度在大于 ９８％时碾压质量合格， 否则为不合格。 将碾压质量评价指标
标准设定为恰好完全隶属于合格的拐点， 考虑到碾压质量直接评价指标的重要性， 因此在施工标准基础
上赋予 １％、 ２％、 ３％的微小变化幅度确定另外 ３ 个拐点， 从而构建干密度、 压实度和 ＣＶ 值的隶属函数。
通过土石坝碾压质量监控系统、 小型气象站获得碾压仓面各个网格的碾压参数和气象参数， 根据
有限随机试坑试验数据得到的料源参数概率分布情况随机生成全仓面的料源参数， 以碾压参数、 料源
参数和气象参数为输入变量， 通过 ＡＣＧＷＯ－ＲＦ 评价模型获得干密度和压实度的预测结果， 并根据划
分网格统计样本值， 通过隶属函数可得每个网格 ｋ（ｋ ＝ １， ２， …， １６ ０００）预测干密度和压实度等碾压
质量评价指标的合格、 不确定、 不合格的隶属度。 根据仓面网格评价判定准则， 确定干密度和压实度

的模糊评价结果， 如图 １０、 １１。 从图中可知， 对干密度预测结果进行模糊评价， 合格的网格占 ９９．８５６％，
不合格为 ０， 不确定性网格占 ０．１４４％； 压实度模糊评价结果中， 碾压质量合格情况占 ９９．００％， 不确

定性占 ０．９３１％， 不合格占 ０．０６９％。 通过二者模糊评价结果可以看到该仓面碾压质量合格率较高。
基于 ２００ 组关仓后的原位试坑试验样本集， 建立压实度 ｐ、 干密度 ｇ 和 ＣＶ 值的线性回归模型， 同
时预留和样本集不相关的 ５０ 组数据作为验证数据集， 获得的回归模型见式（１）。 采用回归模型对样本
集进行预测， 获得 ｐ 和 ｇ 的预测结果与实测值的相关系数 Ｒ 分别为 ０．８６１ 和 ０．８１４， 对验证数据集进行
预测， 相关系数 Ｒ 分别为 ０．７３３ 和 ０．６３７， 结果表明模型预测的精确性均较高， 其中压实度预测效果更

佳， 因此本文采用压实度和 ＣＶ 值的回归模型进行分析。
ＣＶ ＝ ４．３９９×ｐ－４００．３４２； ＣＶ ＝ ２１４．０９１×ｇ－４２５．４９６ （１）
— １ ２ ５ —