Page 117 - 2025年第56卷第2期

３．３ 闸门水力学特性 传统薄壁堰在低水头时易发生贴壁流现象，造成过堰流量测算不准确以及流量
公式与正常堰流不一致的问题 ［２２］ 。采用闸门宽底坎过流结构测流能够有效避免贴壁流发生，从而有助
于解决堰流计算公式不统一的问题。由于测控闸门的结构与矩形薄壁堰差别较大，为明晰闸前水流流
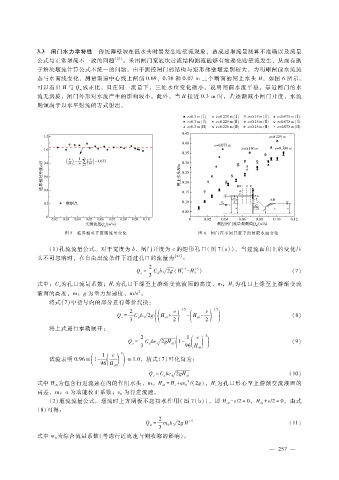
态与水面线变化，测量渠道中心线上闸前 ０．６９、０．３８和 ０．０７ｍ三个断面的闸上水头 Ｈ，如图 ６所示。
可以看出 Ｈ与 Ｑ 成正比，且在同一流量下，三处水位变化微小，说明闸前水流平稳，靠近闸门的水
ｍ
流无涡旋，闸门外形对水流产生的影响较小。此外，当 Ｈ接近 ０．３ｍ时，若逐渐减小闸门开度，水流
则倾向于以水平射流的方式射出。

图 ５ 临界相对开度随流量变化 图 ６ 闸门在不同开度下的闸前水面变化

（１）孔流流量公式。对于宽度为 ｂ、闸门开度为 ｅ的矩形孔口（图 ７（ａ）），当过流面积上的变化压
头不可忽略时，在自由出流条件下通过孔口的流量为 ［２３］ ：
２ １．５ １．５
Ｑ ＝ Ｃｂ ２ｇ（Ｈ － Ｈ ） （７）
ｄ 槡
２
ｏ
１
３
式中：Ｃ为孔口流量系数；Ｈ为孔口下缘至上游渐变流液面的高度，ｍ；Ｈ 为孔口上缘至上游渐变流
２
１
ｄ
２
液面的高度，ｍ；ｇ为重力加速度，ｍ?ｓ。
将式（ ７）中括号内的部分进行等价代换：
２ ｅ １．５ ｅ １．５
ｄ 槡 ((
Ｑ ＝ Ｃｂ ２ｇ Ｈ ＋ ) ( ｃ０ ) ) （８）
－ Ｈ －
ｃ０
ｏ
３ ２ ２
将上式进行泰勒展开：
２ １ ｅ ２
槡 (
Ｑ ＝ Ｃｂｅ ２ｇＨ ｃ０ １ － ( )) （９）
ｄ
ｏ
３ ９６Ｈ ｃ０
( １ ｅ ２
( ))
试验表明 ０．９６ ≤ １ － ９６Ｈ ｃ０ ≤１．０，故式（７）可化简为：
Ｑ ＝ Ｃｂｅ ２ｇＨ （１０）
ｏ ｄ 槡 ｃ０
２
式中 Ｈ 为包含行近流速在内的作用水头，ｍ。Ｈ ＝ Ｈ＋ ａｖ ?（２ｇ），Ｈ为孔口形心至上游渐变流液面的
ｃ
ｃ０
ｃ
０
ｃ０
高差，ｍ；ａ为动能校正系数；ｖ为行进流速。
０
（ ２）堰流流量公式。堰流时上方闸板不起挡水作用（图 ７（ｂ）），即 Ｈ － ｅ?２ ＝ ０，Ｈ ＋ ｅ?２ ＝ ０，由式
ｃ０
ｃ０
（ ８）可得：
２
Ｑ ＝ ｍ ｂ ２ｇＨ １．５ （１１）
０ 槡
ｗ
３
式中 ｍ 为综合流量系数（考虑行近流速与侧收缩的影响）。
０
— ２ ５ ７ —