Page 119 - 2025年第56卷第2期

下非线性回归形式：
槡 ２ Ｈ ｄ
ｍ ＝ ｃ ( ) （１６）
０
２ Ｐ
式中的经验系数 ｃ和 ｄ由试验确定。
（ ２）孔流流量系数。孔口流量系数 Ｃ 的取值制约着孔口出流的性能。闸门孔流的流量系数可以用
ｄ
以下函数关系表示：
Ｃ ＝ Ｇ ｅ，Ｈ，ｇ，ρ ，ｂ，Ｐ ) （１７）
(
ｄ ｃ
［２７］
根据量纲和谐原理，选取 Ｈ、ｇ、ρ 为相互独立的基本物理量，Ｂａｒｅｎｂｌａｔｔ 提出将原有的无量纲
ｃ
群进行组合得到新的无量纲量群，故孔流流量系数的函数关系表示为：
ｅ
( )
Ｃ ＝ Ｇ １ Ｈ ｃ （１８）
ｄ
孔口出流的流量系数可以考虑不同的数学模型 ［２６］ ，本研究选取幂函数与线性函数的组合作为孔口
流量系数的计算模型，因此，式（１８）可变形为：
ｅ
Ｃ ＝ ａ＋ ａ １ ( ) ａ ２ （１９）
ｄ
０
Ｈ
ｃ
式中 ａ（ｉ ＝０ ，１，２）为经验系数，通过试验数据分析确定。式（１９）表明，当闸前水位 Ｙ→ ＋ ∞时，则
ｉ
Ｃ→ａ，这说明当 Ｙ趋于无穷大时，孔口流量系数趋近一个恒定值。
ｄ ０
５ 闸门流量模型

通过试验率定式（１６）和式（１９）中的经验系数，分别构建利用闸门结构测堰流和孔流的流量模型。
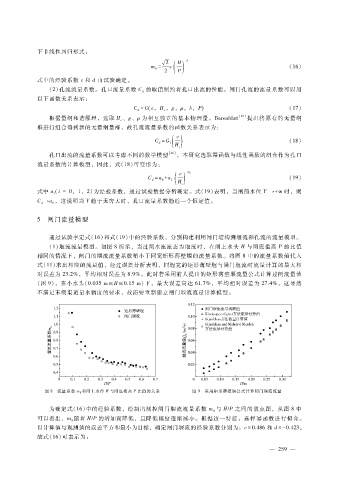
（１）堰流流量模型。如图 ８所示，当过闸水流流态为堰流时，在闸上水头 Ｈ与闸底槛高 Ｐ的比值
相同的情况下，闸门的堰流流量系数稍小于同宽矩形薄壁堰的流量系数。将图 ８中的流量系数值代入
式（１１）求出相应的流量值，经过误差分析表明，同堰宽的矩形薄壁堰与闸门堰流时流量计算的最大相
对误差为 ２３．２％，平均相对误差为 ８．９％。此时若采用前人提出的矩形薄壁堰流量公式计算过闸流量值
（图 ９），在小水头（０．０３５ｍ ≤Ｈ ≤０．１５ｍ）下，最大误差高达 ６１．７％，平均相对误差为 ２７．４％，这显然
不满足末级渠道量水精度的要求，故需要重新建立闸门堰流流量计算模型。

图 ８ 流量系数 ｍ ０ 和闸上水位 Ｈ与闸底槛高 Ｐ比值的关系 图 ９ 采用矩形薄壁堰公式计算闸门堰流流量

为确定式（１６）中的经验系数，绘制出测控闸门堰流流量系数 ｍ 与 Ｈ?Ｐ之间的散点图，从图 ８中
０
可以看出，ｍ 随着 Ｈ?Ｐ的增加而降低，且降低幅度逐渐减小。根据这一特征，选择幂函数进行拟合。
０
以计算值与观测值的误差平方和最小为目标，确定闸门堰流的经验系数分别为：ｃ ＝ ０．４８６ 和 ｄ ＝－ ０．４２３ 。
故式（ １６）可表示为：

— ２ ５ ９ —