Page 121 - 2025年第56卷第2期

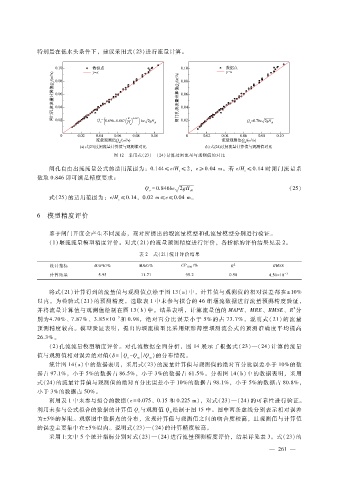
特别是在低水头条件下，建议采用式（２３）进行流量计算。

图 １２ 采用式（２３）—（２４）计算过闸流量与观测值的对比
闸孔自由出流流量公式的适用范围为：０．１４４ ≤ｅ?Ｈ≤２，ｅ ≥０．０４ｍ。若 ｅ?Ｈ≤０．１４时闸门流量系
ｃ
ｃ
数取 ０．８４６即可满足精度要求：
Ｑ ＝ ０．８４６ｂｅ ２ｇＨ （２５）
ｏ 槡 ｃ０
式（ ２５）的适用范围为：ｅ?Ｈ≤０．１４，０．０２ｍ ≤ｅ ≤０．０４ｍ。
ｃ

６ 模型精度评价

鉴于闸门开度会产生不同流态，现对所提出的堰流量模型和孔流量模型分别进行验证。
（１）堰流流量模型精度评价。对式（２１）的流量预测精度进行评价，各指标的评价结果见表 ２。
表 ２ 式（２１）统计评价结果

统计指标 ＭＡＰＥ?％ ＭＲＥ?％ ＣＰ １０％ ?％ Ｒ ２ ＲＭＳＥ
计算结果 ５．９５ １１．７１ ９５．２ ０．９８ ４．５０ × １０ － ３

将式（２１）计算得到的流量值与观测值点绘于图 １３（ａ）中，计算值与观测值的相对误差都在 ±１０％
以内。为检验式（２１）的预测精度，选取表 １中未参与拟合的 ４６组堰流数据进行流量预测精度验证，
２
并将流量计算值与观测值绘制在图 １３（ｂ）中。结果表明，计算流量值的 ＭＡＰＥ、ＭＲＥ、ＲＭＳＥ、Ｒ分
－ ３
别为４．７０％、７．８７％、３．８５ × １０ 和 ０．９８，绝对百分比误差小于 ５％的占 ７３．７％，说明 式（２１）的流量
预测精度较高。模型验证表明，提出的堰流模型比采用矩形薄壁堰测流公式的预测准确度平均提高
２６．３％。
（２）孔流流量模型精度评价。对孔流数据全面分析，图 １４展示了根据式（２３）—（２４）计算的流量
值与观测值相对误差绝对值（ δ ＝ Ｑ － Ｑ ?Ｑ ）的分布情况。
ｏ ｍ ｍ
统计图 １４（ａ）中的数据表明，采用式（２３）的流量计算值与观测值的绝对百分比误差小于 １０％的数
据占 ９７．１％，小于 ５％的数据占 ８６．５％，小于 ３％的数据占 ６１．５％。分析图 １４（ｂ）中的数据表明，采用
式（ ２４）的流量计算值与观测值的绝对百分比误差小于 １０％的数据占 ９８．１％，小于 ５％的数据占 ８０．８％，
小于 ３％的数据占 ５０％。
利用表 １中未参与拟合的数据（ｅ ＝ ０．０７５ 、０．１５和 ０．２２５ｍ），对式（２３）—（２４）的可靠性进行验证。
利用未参与公式拟合的数据的计算值 Ｑ与观测值 Ｑ 绘制于图 １５中。图中两条虚线分别表示相对误差
ｃ ｍ
为±５％的界限。观察图中数据点的分布，发现计算值与观测值之间的吻合度较高，且观测值与计算值
的误差主要集中在±５％以内。说明式（２３）—（２４）的计算精度较高。
采用上文中 ５个统计指标分别对式（２３）—（２４）进行流量预测精度评价，结果详见表 ３。式（２３）的

— ２ ６ １ —