Page 120 - 2025年第56卷第2期

２
槡 Ｈ － ０ ．４２３
ｍ ＝ ( ( ) ) （２０）
０．３４３
０
２ Ｐ
图 ８中的拟合曲线与散点分布比较吻合，使用 Ｆ检验进行了整体显著性检验，选取 ９５％的置信区
间，方差分析结果表明，拟合公式的 Ｆ值为 ２７０２，残差平方和为 ０．０４３，残差均方为 ０．００２，说明拟合
２
效果显著，且修正后的拟合优度 Ｒ 在 ０．９３以上，表明整体拟合效果较好。综上，联立式 （１１）与式
（ １６），得出闸门在自由出流下堰流的流量计算公式为：
Ｈ
Ｑ ＝ ０．３４３ ( ) － ０ ．４２４ 槡 ２ｇｂＨ １．５ （２１）
ｗ Ｐ
闸门堰流流量计算公式的适用范围为：０．０７ ≤Ｈ?Ｐ ≤０．６４，ｂ?Ｂ ＝ ０ ．３０，０．０３５ｍ ≤Ｈ ≤０．３０ｍ。
（２）孔流流量模型。流量系数是衡量闸门过流能力的指标之一，Ｃ 值越大表明通过的流量越多，
ｄ
反之亦然。为了建立统一的孔流模型，需要考虑闸门开度对测流精度的影响。当 ｅ?Ｈ ＞０．１４时，被认
ｃ
为是大孔口出流，由式（ １０）计算流量系数观测值 Ｃ ＝ Ｑ ?（ｂｅ ２ｇＨ ），并研究无量纲量 ｅ?Ｈ 对 Ｃ 值
ｄｍ ｍ 槡 ｃ０ ｃ ｄ
的响应。对孔流数据全面分析表明，式（１９）与试验数据之间显著相关且拟合精度最高。上述结论与
［２５］
Ｈｕｓｓａｉｎ 以及 Ｖａｔａｎｋｈａｈ ［２６，２８］ 等学者的研究成果一致。对 １３４组孔流数据进行拟合，得出闸门开度为
大孔口时的流量系数计算式如下：
ｅ
Ｃ ＝ ０．６９６ － ０．００７ ( ) － ０ ．６９４ （２２）
ｄ
Ｈ
ｃ
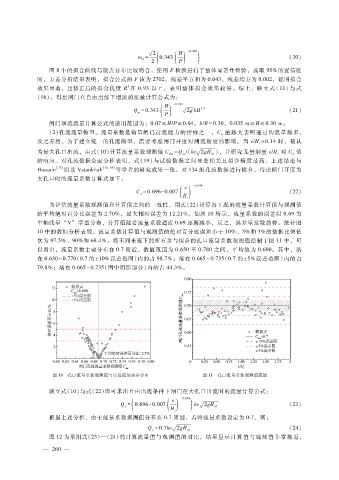
为评估流量系数观测值和计算值之间的一致性，用式（２２）计算各工况的流量系数计算值与观测值
的平均绝对百分比误差为 ２．７０％，最大相对误差为 １２．２１％，如图 １０所示，流量系数的误差以 ０．６９为
中轴线呈 “ Ｖ” 字型分布，计算值随着流量系数逼近 ０．６９逐渐减小，反之，误差呈发散趋势。统计图
１０中的数据分析表明，流量系数计算值与观测值的绝对百分比误差小于 １０％、５％和 ３％的数据比例依
次为 ９７．５％、９０％和 ６８．４％。将不同来流下的所有参与拟合的孔口流量系数观测值绘制于图 １１中，可
以看出，流量系数主要分布在 ０．７附近，数值范围为 ０．６５０至 ０．７８０之间，平均值为 ０．６９０。其中，落
在 ０．６３０～０．７７０（０．７的±１０％误差范围）内的占 ９８．７％；落在 ０．６６５～０．７３５（０．７的±５％误差范围）内的占
７９．８％；落在 ０．６６５～０．７３５（图中阴影部分）内的占 ４４．３％。

图 １０ 孔口流量系数观测值与计算值的误差分布 图 １１ 孔口流量系数观测值范围

联立式（１０）与式（２２）即可求出自由出流条件下闸门在大孔口出流时的流量计算公式：
－ ０ ．６９４
ｅ
(
ｂｅ ２ｇＨ
Ｑ ＝ ０．６９６ － ０．００７ ( ) ) 槡 ｃ０ （２３）
ｏ
Ｈ
ｃ
根据上述分析，由于流量系数观测值分布在 ０．７周围，若将流量系数设定为 ０．７，则：
Ｑ ＝ ０ ．７ｂｅ ２ｇＨ （２４）
ｏ 槡 ｃ０
图 １２为采用式（２３）—（２４）的计算流量值与观测值的对比，结果显示计算值与观测值非常接近，
— ２ ６ —
０