Page 12 - 2025年第56卷第2期

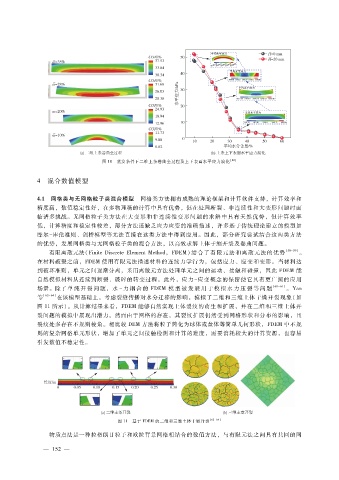
图 １０ 蒸发条件下二维土条卷曲全过程及上下表面水平应力演化 ［４８］

４ 混合数值模型

４．１ 网格类与无网格粒子类混合模型 网格类方法拥有成熟的理论框架和计算软件支持，计算效率和
精度高，数值稳定性好，在多物理场的计算中具有优势，但在处理断裂、非连续性和大变形问题时面
临诸多挑战。无网格粒子类方法在大变形和非连续性变形问题的求解中具有天然优势，但计算效率
低，计算精度和稳定性较差，部分方法还缺乏应力应变的准确描述，许多基于传统理论建立的模型如
摩尔－ 库伦准则、剑桥模型等无法直接在这类方法中得到应用。因此，部分研究尝试结合这两类方法
的优势，发展网格类与无网格粒子类的混合方法，以高效求解土体干缩开裂及卷曲问题。
有限离散元法（ ＦｉｎｉｔｅＤｉｓｃｒｅｔｅＥｌｅｍｅｎｔＭｅｔｈｏｄ，ＦＤＥＭ）结合了有限元法和离散元法的优势 ［５８ － ５９］ 。
在材料破裂之前，ＦＤＥＭ使用有限元法描述材料的连续力学行为，包括应力、应变和变形。当材料达
到破坏准则，单元之间逐渐分离，采用离散元方法处理单元之间的运动、接触和碰撞，因此 ＦＤＥＭ能
自然模拟材料从连续到断裂、破碎的转变过程。此外，应力 － 应变概念的保留使它具有更广阔的应用
场景。除了 单 纯 开 裂 问 题，水 － 力 耦 合 的 ＦＤＥＭ 模 型 被 发 展 用 于 模 拟 水 力 压 裂 等 问 题 ［６０ － ６１］ 。 Ｙａｎ
等 ［６２ － ６４］ 在该模型基础上，考虑裂缝传播对水分迁移的影响，模拟了二维和三维土体干燥开裂现象（如
图 １１所示）。从计算结果来看，ＦＤＥＭ能够自然实现土体裂纹的萌生和扩展，并在二维和三维土体开
裂问题的模拟中展现出潜力。然而由于网格的存在，其裂纹扩展仍然受到网格形状和分布的影响，且
裂纹处多存在不规则棱角。相比较 ＤＥＭ方法将粒子简化为球体或盘体等简单几何形状，ＦＤＥＭ中不规
则的复杂网格单元形状，增加了单元之间接触检测和计算的难度，需要消耗较大的计算资源，也容易
引发数值不稳定性。

图 １１ 基于 ＦＤＥＭ的二维和三维土体干缩开裂 ［６２ － ６４］

物质点法是一种拉格朗日粒子和欧拉背景网格相结合的数值方法，与有限元法之间具有共同的网

— １ ５ —
２