Page 8 - 2025年第56卷第2期

并讨论了土层厚度、蒸发强度对卷曲程度的影响。Ｌｉｎ等 ［３７ － ３８］ 基于离散元方法，进一步考虑除土条上
表面以外的其他边界额外水分蒸发，计算模拟了向上卷曲和向下卷曲两种卷曲状态。

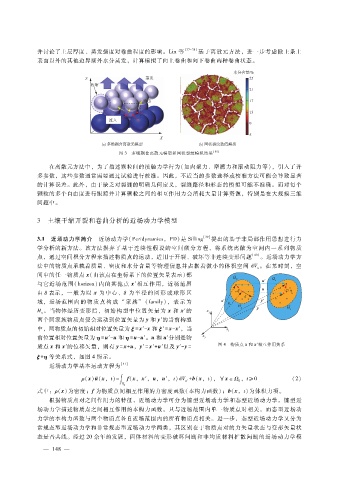
图 ３ 多场耦合离散元模型和网状裂纹模拟结果 ［３５］

在离散元方法中，为了描述颗粒间的接触力学行为（如内聚力、摩擦力和滚动阻力等），引入了许
多参数，这些参数通常需要通过试验进行校准。因此，不适当的参数选择或校准方法可能会导致显著
的计算误差。此外，由于缺乏对裂缝的明确几何定义，裂缝路径和形态的模拟可能不准确。而对每个
颗粒的多个自由度进行跟踪并计算颗粒之间的相互作用力会消耗大量计算资源，特别是在大规模三维
问题中。

３ 土壤干缩开裂和卷曲分析的近场动力学模型

［３９］
３．１ 近场动力学简介 近场动力学（Ｐｅｒｉｄｙｎａｍｉｃｓ，ＰＤ）是 Ｓｉｌｌｉｎｇ 提出的基于非局部作用思想进行力
学分析的新方法。该方法摒弃了基于连续性假设的空间微分方程，将系统离散为空间内一系列物质
点，通过空间积分方程来描述物质点的运动，适用于开裂、破坏等非连续变形问题 ［４０］ 。近场动力学方
法中的物质点承载着质量、密度和水分含量等物理信息并占据着微小的体积空间 ｄＶ。在某时刻，空
ｘ
间中的任一物质点 ｘ（由该点在坐标系下的位置矢量表示）都
与它近场范围（ ｈｏｒｉｚｏｎ）内的其他点 ｘ′相互作用，近场范围
由 δ 表示，一 般为 以 ｘ为中心、δ 为半 径 的 圆 形 或 球 形 区
域，近场范 围 内 的 物 质 点 构 成 “家 族” （ｆａｍｉｌｙ），表 示 为
Ｈ。当物体经历变形后，初始构型中位置矢量为 ｘ和 ｘ′的
ｘ
两个同家族物质点便会运动到位置矢量为 ｙ和 ｙ′的当前构型
中，两物质点的初始相对位置矢量为 ξ ＝ ｘ′ － ｘ和 ξ ′ ＝ ｘ － ｘ′，当
前位置相对位置矢量为 η ＝ ｕ′ － ｕ和 η ＝ ｕ － ｕ′。ｕ和 ｕ′分别是物
质点 ｘ和 ｘ′的位移矢量，则有 ｙ ＝ ｘ ＋ ｕ，ｙ′ ＝ ｘ′ ＋ ｕ′以及 ｙ′ － ｙ ＝ 图 ４ 物质点 ｘ和 ｘ′相互作用关系

ξ ＋ η等关系式，如图 ４所示。
近场动力学基本运动方程为 ［４１］
∫ ，ｔ ≥０ （２）
ρ （ｘ）ü（ｘ，ｔ） ＝ ｆ（ｘ，ｘ′，ｕ，ｕ′，ｔ）ｄＶ ＋ ｂ（ｘ，ｔ），ｘ ∈Ω ０
ｘ′
Ｈ ｘ
式中：ρ （ｘ）为密度；ｆ为物质点间相互作用的力密度函数（本构力函数）；ｂ（ｘ，ｔ）为体积力项。
根据物质点对之间作用力的特征，近场动力学可分为键型近场动力学和态型近场动力学。键型近
场动力学描述物质点之间相互作用的本构力函数，只与近场范围内单一物质点对相关，而态型近场动
力学的本构力函数与两个物质点各自近场范围内的所有物质点相关。进一步，态型近场动力学又分为
常规态型近场动力学和非常规态型近场动力学两类，其区别在于物质点对的力矢量状态与变形矢量状
态是否共线。经过 ２０余年的发展，固体材料的变形破坏问题和非均质材料扩散问题的近场动力学模

— １ ４ —
８