Page 10 - 2025年第56卷第2期

Ｔ
[ ][] [ Ｕ ] （８）
Φ
Ｕ
Ｋ Ｇ
＝－
０
λ
Ｇ
式中：Ｋ为所有物质点的刚度矩阵；Ｕ为所有物质点的位移矩阵；Ｇ为已知系数矩阵；λ为拉格朗日

乘子；Ｕ 为已知边界条件。
［５３］
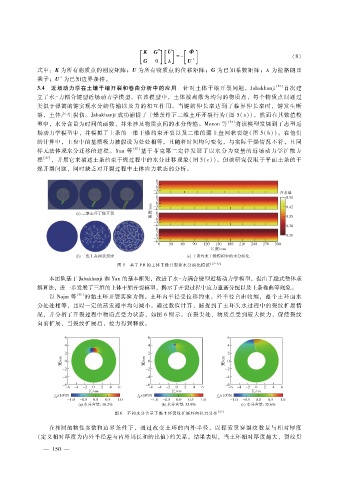
３．４ 近场动力学在土壤干缩开裂和卷曲分析中的应用 针对土体干缩开裂问题，Ｊａｂａｋｈａｎｊｉ 首次建
立了水－ 力耦合键型近场动力学模型。在该模型中，土体被离散为均匀的物质点，每个物质点间通过
类似于弹簧的键实现水分的传输以及力的相互作用。当键的伸长率达到了临界伸长率时，键发生断
裂，土体产生损伤。Ｊａｂａｋｈａｎｊｉ成功捕捉了干燥条件下二维土环开裂行为（图 ５（ａ）），然而在其数值模
型中，水分含量为时间的函数，并未涉及物质点间的水分传输。Ｍｅｎｏｎ等 ［５４］ 将该模型发展到了态型近
场动力学模型中，并模拟了土条的一维干燥约束开裂以及二维的薄土盘网状裂缝（图 ５（ｂ））。在他们
的计算中，土盘中的基质吸力被假设为处处相等，且随着时间均匀变化，与实际干燥情况不符，且同
样无法体现水分迁移的过程。Ｙａｎ等 ［５５］ 基于菲克第二定律发展了以水分为变量的近场动力学扩散方
程 ［４７］ ，并用它来描述土条约束干燥过程中的水分迁移现象（图 ５（ｃ））。但该研究仅限于平面土条的干
燥开裂问题，同时缺乏对开裂过程中土体应力状态的分析。

图 ５ 基于 ＰＤ的土体干燥开裂和水分演化模拟 ［５３ － ５５］

本团队基于 Ｊａｂａｋｈａｎｊｉ和 Ｙａｎ的基本框架，改进了水－ 力耦合键型近场动力学模型，提出了隐式整体求
解算法，进一步发展了三维的土体干缩开裂模型，揭示了开裂过程中应力重新分配以及土条卷曲等现象。
以 Ｎａｊｍ等 ［５６］ 的黏土环开裂实验为例。土环内半径受位移约束，外半径自由收缩，整个土环面水
分处处相等，且以一定的蒸发速率均匀减小。通过数值计算，捕捉到了土环失水过程中的裂纹扩展情
况，并分析了开裂过程中物质点受力状态，如图 ６所示。在裂尖处，物质点受到较大拉力，促使裂纹
向前扩展，当裂纹扩展后，拉力得到释放。

［５１］
图 ６ 不同水分含量下黏土环裂纹扩展环向拉力分布
在相同的物性参数和边界条件下，通过改变土环的内外半径，以探索贯穿裂纹数量与相对厚度
（定义相对厚度为内外半径差与内外周长和的比值）的关系。结果表明，当土环相对厚度越大，裂纹贯

— １ ５ —
０