Page 32 - 2025年第56卷第2期

浮物撞击与预应力钢丝断裂开展，采用齿轮切割机切割预应力钢丝的方式，模拟氢脆作用下的断丝信
号；使用锤子击打 ＰＣＣＰ内壁，模拟水中漂浮物对 ＰＣＣＰ的碰撞。另外，为模拟预应力钢丝同时断裂
的情况，在切割断丝时，设置 ２种工况，即仅切断 １根钢丝以及同时切断 ２根钢丝，振动信号分别记
作断丝－ １ 信号和断丝－ ２ 信号。
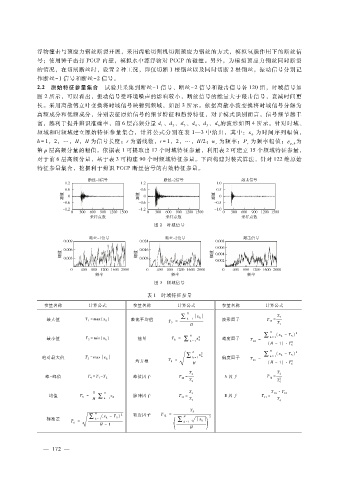
２．２ 原始特征参量集合 试验共采集到断丝－ １ 信号、断丝－ ２ 信号和敲击信号各 １２０组，时域信号如
图 ２所示，可以看出，振动信号受环境噪声的影响较小，断丝信号的能量大于敲击信号，衰减时间更
长。采用离散傅立叶变换将时域信号映射到频域，如图 ３所示。依据离散小波变换将时域信号分解为
高频成分和低频成分，分别表征原始信号的细节特征和趋势特征，对于模式识别而言，信号细节越丰
富，越利于提升辨识准确率，前 ６层高频分量 ｄ、ｄ、ｄ、ｄ、ｄ、ｄ的波形如图 ４所示。针对时域、
１ ２ ３ ４ ５ ６
频域和时频域建立原始特征参量集合，计算公式分别在表 １—３中给出，其中：ｘ 为时间序列幅值，
ｈ
为
ρ
ｒ
ｈ ＝ １ ，２，…，Ｈ，Ｈ为信号长度；ｒ为谱线数，ｒ ＝ １ ，２，…，Ｈ?２；ｗ 为频率；Ｐ 为频率幅值；ε ，ｈ
ｒ
第 ρ 层高频分量的幅值。依据表 １可提取出 １７个时域特征参量，利用表 ２可建立 １５个频域特征参量，
对于前 ６层高频分量，基于表 ３可构建 ９０个时频域特征参量。下面构建封装式算法，针对 １２２维原始
特征参量集合，挖掘利于辨识 ＰＣＣＰ断丝信号的有效特征参量。

图 ２ 时域信号

图 ３ 频域信号
表 １ 时域特征参量

参量名称 计算公式 参量名称 计算公式 参量名称 计算公式
Ｈ
∑ ｘ ｈ Ｔ ９
＝
最大值 Ｔ １ ｍａｘ （ｘ ｈ ） 整流平均值 ｈ ＝１ 波形因子 Ｔ １３ ＝
Ｔ ７ ＝
Ｈ Ｔ ７
Ｈ ４
Ｈ ∑ （ｘ ｈ －Ｔ ５ ）
＝
＝
最小值 Ｔ ２ ｍｉｎ （ｘ ｈ ） 能量 Ｔ ８ ∑ ｘ ｈ ２ 峭度因子 ＝ ｈ ＝１
ｈ ＝１ Ｔ １４
４
（Ｈ－１）·Ｔ ６
Ｈ
Ｈ －Ｔ ５ ） ３
２
∑ ｘ ｈ ∑ （ｘ ｈ
＝
绝对最大值 Ｔ ３ ｍａｘ ｘ ｈ ｈ ＝１ 偏度因子 ＝ ｈ ＝１
均方根 Ｔ ９ ＝ 槡 Ｈ Ｔ １５ （Ｈ－１）·Ｔ ６
３
Ｔ ３ Ｔ ３
＝ －
峰－ 峰值 Ｔ ４ Ｔ １ Ｔ ２ 峰值因子 Ｔ １０ ＝ Ａ因子 Ｔ １６ ＝
３
Ｔ ９ Ｔ ６
１ Ｈ Ｔ ３ Ｔ １４ ·Ｔ １０
均值 Ｔ ５ ＝ ∑ ｘ ｈ 脉冲因子 Ｔ １１ ＝ Ｂ因子 Ｔ １７ ＝
Ｈ ｈ ＝１ Ｔ ７ Ｔ ６
Ｔ ３
Ｈ ２ 裕度因子 Ｔ １２ ＝
∑ （ｘ ｈ －Ｔ ５ ） Ｈ ２
标准差 ＝ ｈ ＝１ ∑ ｘ ｈ
槡 Ｈ－１ Ｈ
Ｔ ６ ( ｈ ＝１槡 )
— １ ７ —
２